The three Kolmogorov axioms underpin probability theory. Before we explore the axioms, some common probability language will be introduced.
An experiment is a process of observation where the output cannot be predicted with certainty due to random effects. Example: rolling a dice.
A trial is a single occurrence of an experiment. Multiple trials of an experiment can form a new experiment. Example: an experiment consists of rolling a dice twice and the trial is one instance of the twice-rolled dice experiment.
An outcome is an observed output of a trial. Examples: rolling a 3 or rolling a 1 and 5 in the twice-rolled dice experiment.
The sample space Ω is the set of all possible outcomes of an experiment. Examples: each side of the dice or ordered pairs of twice-rolled dice experiments.
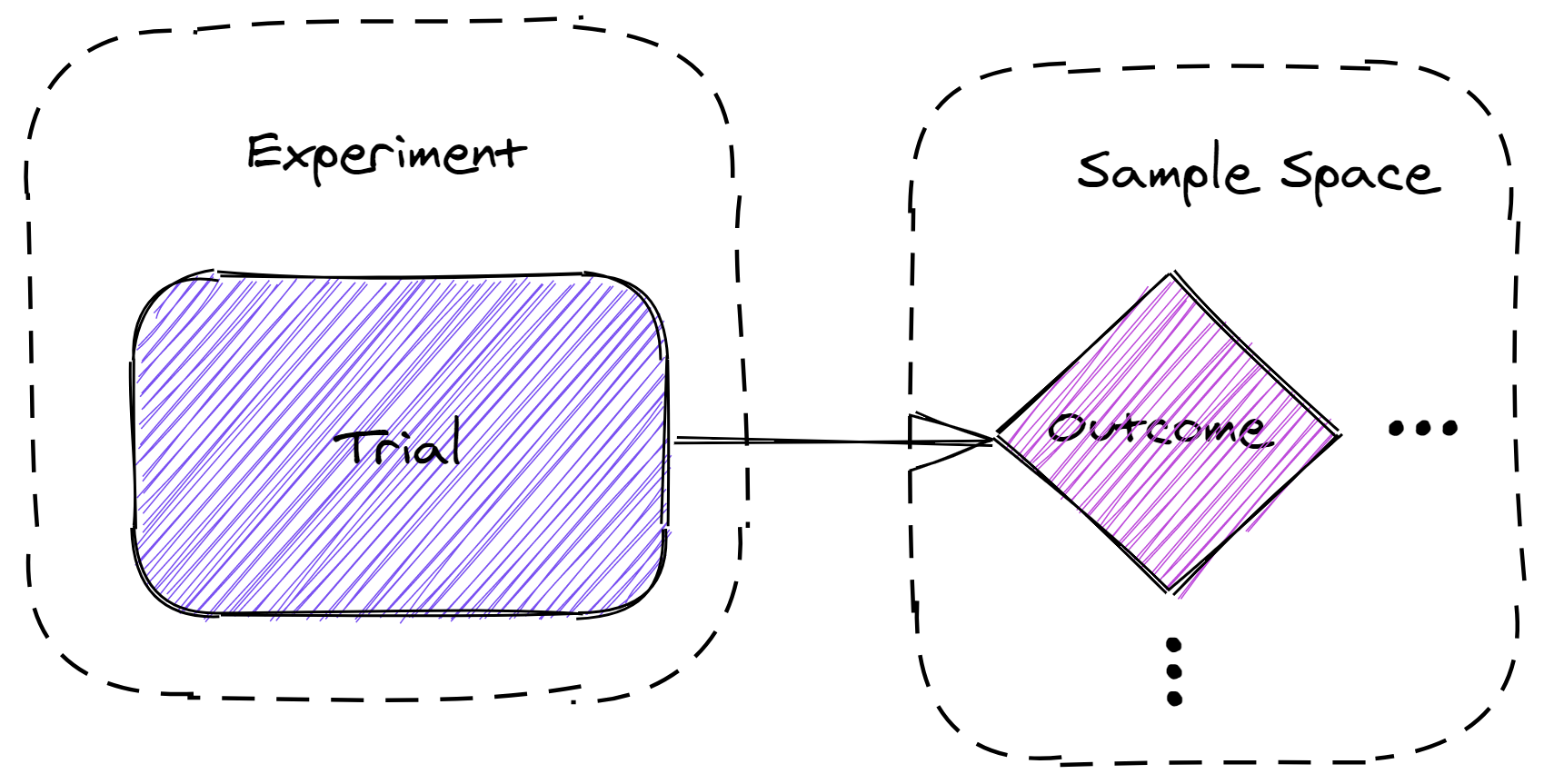
An event A is a subset of outcomes in the sample space Ω. Examples: rolling a side less than 4, rolling an even number or rolling a 2 and then a 3.

The operations of set theory apply to events. The union of events is the set of outcomes in A, B or both. The intersection of events is the set of outcomes in both A and B.

The event consisting of no outcomes is called the null event. If events A and B have no outcomes in common then A and B are disjoint events (mutually exclusive).
A Probability measure P is a function that assigns a real number to each measurable event. A probability measure must follow the axioms of probability.
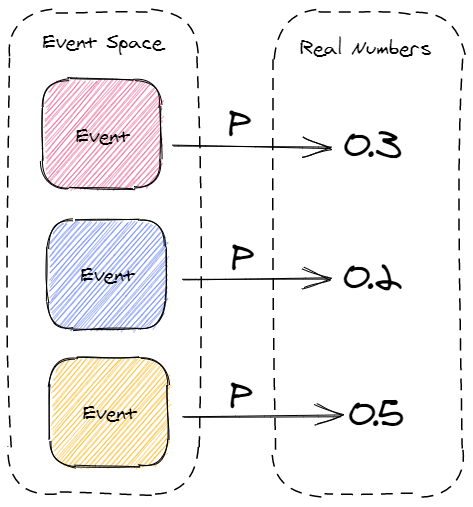
Now we will explore the three axioms of probability.
First axiom: non-negative, real number
The probability of an event is a non-negative real number.

This axiom means that the smallest probability of an event is zero. It does not specify an upper bound, however a probability theorem does.
Second axiom: unitarity
The probability that at least one outcome in the sample space will occur is 1.

This axiom means that it is certain that an outcome will occur from observing an experiment.
Third axiom: countable additivity
If there is an infinite set of disjoint events in a sample space Ω then the probability of the union of events is equal to the sum of probabilities of all events.
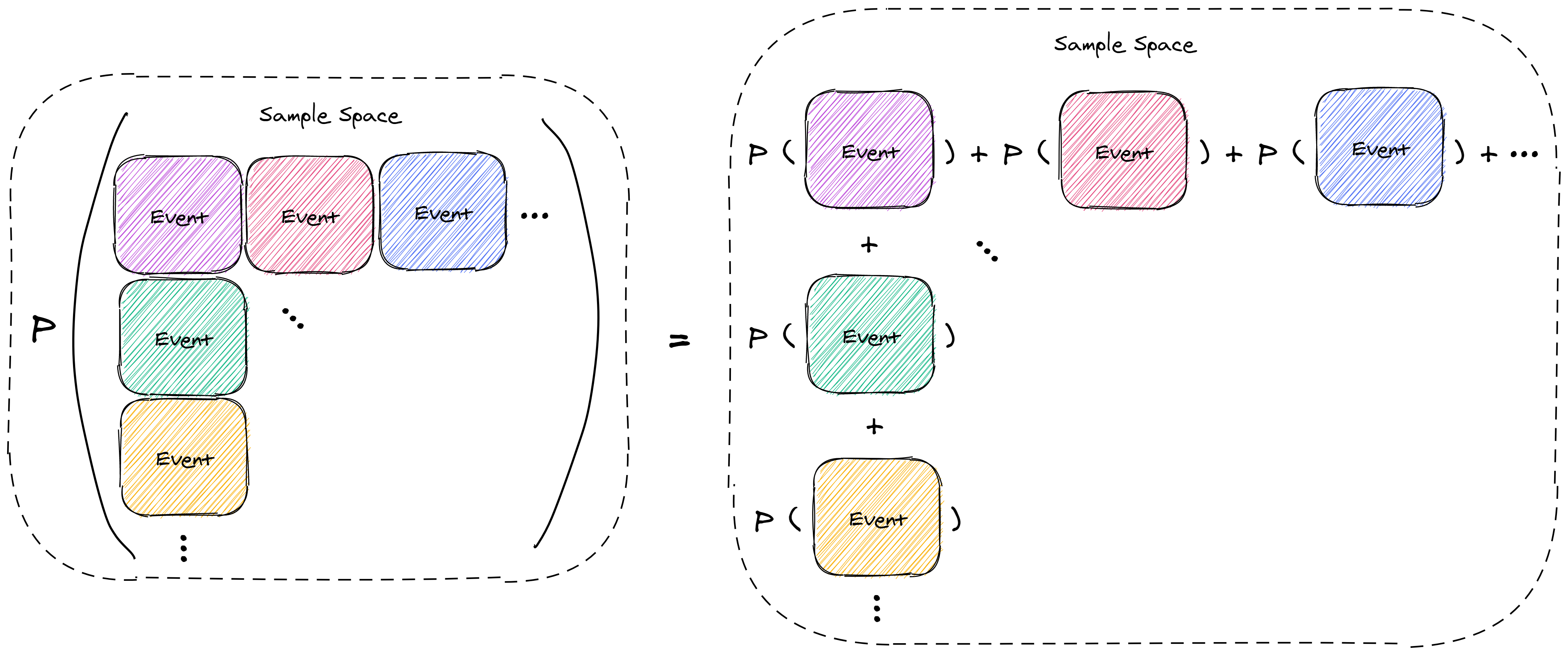
This axiom forms a relationship between a set of disjoint events in a sample space and the individual probabilities of each event. A probability theorem shows how a finite set of disjoint events can be represented as an infinite set too.
The axioms of probability can subsequently be used to derive the theorems of probability.








