Getting Started
You have precious data. Be it videos of your baby’s first steps or documents you’ve scanned for a paperless life or information you store for users of your startup product. You want to keep this data safe, of course. Safe from permanent loss, temporary unavailability, and unauthorized access.

A typical practice is to replicate your data and spread the replicas across storage domains that have uncorrelated failures. So, for example, you store a copy of your video in three different cloud storage providers. This is a perfectly reasonable way to keep your data safe. But it has two main drawbacks:
- Replication is costly. For example, when you store 3 copies of the same video, you have to pay for 3 bytes of storage per byte of source data.
- Securing a replica is hard. Since each replica is a full copy, it is vulnerable to illicit security breaches as well as lawful access by the service provider or law enforcement in conformance with the stated privacy policy. A guard against this is encryption, but that comes with key-management complexity that is beyond the scope of many.
There is a better way. It’s a way that is well known and well used by experts in sophisticated storage and networking systems. It’s called Erasure Coding. In this article, my hope is to democratize Erasure Coding, releasing it from niche usage into ubiquity. The questions to explore are:
- What is Erasure Coding?
- Why is it better than Replication?
- How can you use Linear Algebra to erasure code?
- How can you use Prime Fields for lossless finite-precision encoding?
- How can you use Extension Fields to encode arbitrary binary data?
- How can you use binary matrices to encode efficiently?
- How can you implement all of this?
1. What Is Erasure Coding?
An [N, K] erasure code encodes source data into N shards (N ≥ 1). Each shard is 1/K the size of the source data (1 ≤ K ≤ N). The source data can be decoded from any K of the encoded shards. So the code can tolerate the loss of any N-K shards without incurring any source data loss. This durability comes at the cost of redundancy: every source byte is inflated by a factor of N/K. An [R, 1] erasure code is simply R-way replication.
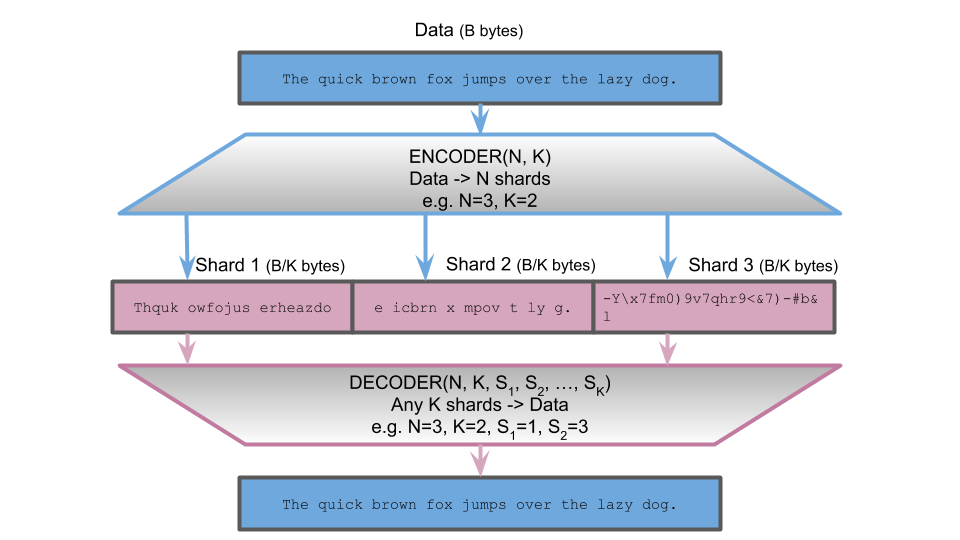
Figure 1 shows the example of a [3, 2] erasure code using an actual prototype implementation. The source data is the well-known pangram "The quick brown fox jumps over the lazy dog". It is 44 characters (bytes) long. The encoder encodes it into 3 shards, each shard being 22 characters (bytes) long. Any 2 of the shards can be used to reconstruct the original pangram.
2. Why Is It Better Than Replication?
The bottom line is that erasure coding is fundamentally more secure than replication and is cheaper.
How is erasure coding more secure than replication? Since each encoded shard in an [N, K] code is 1/K the size of the source data, each shard has 1/K of the information in the source data. Here "information" is used in the technical sense of "Shannon information" from Information Theory (https://en.wikipedia.org/wiki/Information_theory). So, as long as K > 1, it is impossible (in the absolute sense) to get the source data from a single shard. For example, if you store each shard in a different cloud service, no single service would have access to your source data, even in principle. No encryption needed!

Figure 2 illustrates that if the source data is an image of my puppy, Abby, none of the encoded shards will reveal that. In fact, the shards won’t even correspond to a coherent image format, but instead will just be blobs of binary data.
How is erasure coding cheaper than replication? Consider the scenario in which you are willing to store your data in some number (‘S’) of cloud storage providers. And you want to tolerate the loss/unavailability of any subset ‘F’ of the providers. If you use replication, you will have to replicate your data at least (F+1) times, leading to an inflation of (F+1) stored bytes for every source data byte. If you use erasure coding, you can reduce data inflation without sacrificing the required durability. The optimal code that achieves that is a [S, S-F] code which has a redundancy factor of S/(S-F). The savings in storage is tabulated below for several values of S (the number of storage providers) and F (the number of losses to tolerate):

Figure 3 below illustrates how an image of my puppy is encoded into 4 shards using a [4, 2] erasure code. Each shard is stored in a different cloud store. A shard is half the size of the image, leading to a total stored size of twice the image size. With this scheme, the image can tolerate the loss of any 2 cloud stores. If instead the image was stored using replication, then it would need at least 3 replicas to survive the loss of any 2 stores. So erasure coding reduces storage by 33% (from 3x to 2x per source byte) compared to the equivalent replication scheme to tolerate 2 outages.

How Can You Use Linear Algebra To Erasure Code?
If you want to erasure code your data, you have to dive into the "More Math…" part in the subtitle of this article. To make the mathematical concepts more accessible, you’ll build up an example [3, 2] erasure code to encode a melody written in the 7-letter musical alphabet from A to G. The small size of the alphabet makes it easier to illustrate the math involved without getting bogged down in large numbers. We’ll encode the melody for the line "Happy birthday to you", which is "CCDCFE".
If you want to [N, K] erasure-code your data, you start by processing the source data stream in fixed-size blocks of data. Each data-block consists of K equal-sized chunks. Figure 4 illustrates how this chunking and blocking works for the example melody data.

Since each chunk has a fixed size, you can define a numerical representation for the chunks. Then, each data-block specifies a K-component vector in a K-dimensional vector space. Figure 5 shows the numerical representation and data-block vectors for the example.

Erasure coding is a linear transformation from each K-component data-block vector to its corresponding N-component code-block vector. The code-block chunks are striped across the N encoded shards i.e. each code-chunk is appended to the corresponding shard. The linear transformation of a data-block into a code-block can be represented by an N by K matrix.
Will any N by K encoder matrix work? Of course not. The matrix must have one crucial property. If you want to reconstruct the K chunks of a data-block from any K of N chunks of the corresponding code-block, you need every K by K submatrix of the encoder matrix to have an inverse matrix. Each such inverse matrix is the decoder matrix for the corresponding K chunks of a code-block.
How can you construct an N by K matrix such that every K by K submatrix has an inverse? Recall that a square matrix has an inverse if and only if its determinant is non-zero. So the encoder must have a non-zero determinant for every K by K submatrix. One way to achieve this is to use a Cauchy matrix (https://en.wikipedia.org/wiki/Cauchy_matrix). How? Choose a set of N distinct numbers {x₁, x₂, …, xₙ} and a non-overlapping set of K distinct numbers {y₁, y₂, …, yₖ}. Then, the matrix element in the ith row and kth column is 1/(xᵢ-yⱼ). The determinant of the K by K square submatrix with the K rows {r₁, r₂, …, rₖ} selected is non-zero and is given by the following:
We covered a lot of ground above. Let’s illustrate all of that in our example of the "Happy birthday" melody. Figure 6 constructs a 3 by 2 Cauchy encoder matrix for the [3, 2] erasure code used in the example.

Figure 7 shows how the vectors for the 3 data-blocks ("CC", "DC", "FE") are encoded into 3 code-blocks (each with 3 chunks) and how the chunks in each code-block are striped across the encoded shards.

Figure 8 shows all the decoder matrices for the example, for each of the 3 ways in which 2 shards can be picked out of 3.

Figure 9 shows how each pair of shards decodes into the source data using the corresponding decoder matrix.

There you have it. You now know how to use Linear Algebra to erasure code your data. To recap the main ideas, an [N, K] erasure code maps a K-chunk data-block in a K-dimensional vector space to an N-chunk code-block in a K-dimensional subspace of an N-dimensional vector space. The code-chunks in a code-block are striped across the code shards. The map is specially constructed, using a Cauchy matrix, to be reversible for any K-chunk subset of the N-chunk code-blocks, allowing the source data to be decoded from any K code shards.
How Can You Use Prime Fields For Lossless Finite-precision Encoding?
You now know the theory behind erasure coding. What happens when this theory meets reality?
In theory there’s no difference between theory and practice. In practice there is.
There is a high practical hurdle to surmount. The 7-letter musical alphabet requires only the integers 0 to 6 to represent any data chunk. However, a code chunk is a full-blown rational number. Such code chunks cannot be represented exactly by the finite precision in computer systems. For example, the code chunk 5/3 has the infinitely repeating binary representation 1.101010101… This makes the encoding lossy and dooms the decoding.
How can you solve the finite precision problem? "More Math…" comes to the rescue again. Instead of using rational numbers in the encoder matrix, use numbers from a finite field. A field is a set of numbers on which arithmetic is well defined. That means that addition, subtraction, multiplication, and division behave in the same way as they do in real numbers or rational numbers. This behavior consists of several properties like closure, associativity, commutativity, distributivity, identity, inverse, and so on. The technical details are not particularly relevant for this article, so let’s gloss over them (see "A Finite Number Of Numbers" if you’re interested). A finite field is a field that has a finite number of numbers, unlike the infinitely large fields of real numbers and rational numbers that you’re more used to.
Which finite field should you use to erasure code your data? For starters, use a Prime Field. A Prime Field has ‘p’ numbers 0, 1, 2, …, p-1 for any prime number ‘p’. Addition and multiplication proceed as if the numbers are integers. If the result is larger than p-1, then it is mapped back into the finite field by dividing the result by p and using the remainder as the result. Another way to think about this is that the numbers are laid out clockwise in increasing order on a number-circle and addition proceeds by clockwise hops. Subtracting a number is defined as adding the negative of that number. The negative of a number ‘a’ is the number ‘b’ that satisfies ‘a’ + ‘b’ = 0. For a prime p-field, ‘-a’ = ‘p’-‘a’. Dividing by a non-zero number is defined as multiplying by the reciprocal of that number. The reciprocal of a number ‘a’ is the number ‘b’ that satisfies ‘a’ * ‘b’ = 1.
Which prime number should you choose for the Prime Field? A large enough one to represent each data chunk. Also, it should have at least N+K numbers to construct the Cauchy encoder matrix.
For the 7-letter musical alphabet example, the Prime Field with 7 numbers is just large enough. The field can represent every data chunk since each chunk takes on one of 7 values in the musical alphabet. And, for a [3, 2] code we have the 5 numbers needed to construct the Cauchy encoder. Here’s a cheat-sheet of how to do arithmetic in the 7-field:

Here’s the [3, 2] encoding of "CCDCFE" over the 7-field, and decoding from shards 2 and 3:

So, by using a Prime Finite Field of numbers, each chunk can be represented exactly within the finite precision available on a computer and you can merrily perform the arithmetic to encode and decode without any loss of information due to rounding errors and such.
How Can You Use Extension Fields To Encode Arbitrary Binary Data?
You have solved the problem of information loss due to finite precision arithmetic by using numbers in a Prime Field. But you still have a practical hurdle to surmount, albeit a lower one than before. To chunk up binary data into a sequence of numbers in a prime field, you’ll end up needing extra bits per chunk. For example, to convert a sequence of bits (1s and 0s) into a 7-field number, you can convert at most 2 bits at a time into 7-field numbers (since using 3 bits will take on 2³ values, which is 1 too many for the 7-field). And, at least 3 bits are needed to represent a 7-field number (with one permutation of the 3 bits, 111, being unused). So the chunking would inflate every 2 bits of data into 3 bits in a data chunk. Surely you don’t want to needlessly pay for this extra storage, especially given that one of the main benefits of erasure coding is to reduce storage costs without sacrificing durability.
How can you solve the problem of chunking inflation caused by Prime Fields not being aligned with binary representations? Can "More Math…" help you out again? Yes! An n-bit string can be thought of as a number in a base-2 number system with values between 0 and 2ⁿ-1. Do these numbers satisfy the properties of a finite field? As luck would have it, they do. For every prime number ‘p’ and whole number ‘n’, there is a pⁿ-field called an Extension Field with the numbers 0, 1, 2, …, pⁿ-1. Such fields follow different rules of arithmetic than the take-the-remainder approach of Prime Fields. Arithmetic is done by representing each number as a polynomial of degree < n with coefficients in a p-field. Then, two numbers can be added by adding their polynomials. Similarly, two numbers can be multiplied by multiplying their polynomials. However, the multiplication can yield a polynomial of degree ≥ n. In that case, the polynomial is divided by an irreducible polynomial of degree n, and the remainder polynomial of degree < n is taken as the result. This is analogous to how a result larger than p-1 is handled in a prime p-field. Arithmetic using polynomials over a prime field may be a lot to digest for some of you. If you want to spend more time with this, take a look at "A Finite Number Of Numbers". For this article, let’s go full steam ahead with 2ⁿ-fields whose numbers are n-bit strings.
For the 7-letter musical alphabet example, we can use the extension 2³-field with 8 numbers. This field can represent every data chunk since each chunk takes on one of 7 values in the musical alphabet and we have 8 available numbers in the field. And, for a [3, 2] code we have the 5 numbers needed to construct the Cauchy encoder. Here’s a cheat-sheet of how to do arithmetic in the 2³-field:

Here’s the [3, 2] encoding of "CCDCFE" over the 2³-field, and decoding from shards 2 and 3:

So, using 2ⁿ-fields of numbers, the code chunks and data chunks are n-bit strings with exact n-bit representations on a computer and no inflation due to chunking.
How Can You Use Binary Matrices To Encode Efficiently?
You now have everything you need to go ahead and implement your own erasure codes using numbers in a 2ⁿ Extension Field. Time to go home? You can if you want. But do you really want to spend computational time and resources on expensive matrix multiplications for every block in your data? Would you like to go a bit further and implement a solution that reduces to performing primitive XORs ("exclusive ors") on specific word-length chunks of binary data?
The trick is to represent the numbers in a 2ⁿ-field as n by n matrices whose elements are 2-field numbers (0 and 1). Then, addition and multiplication follow the usual matrix addition and multiplication, except using the 2-field rules. What is the matrix representation of the numbers? Think of each n-digit base-2 number in the 2ⁿ-field as an n-component vector in an n-dimensional vector space over the 2-field. The vector space is spanned by the n-component basis vectors (1, 0, …, 0), (0, 1, 0, …, 0), …, (0, 0, …, 0, 1). For example, in the case of the 2³-field, 000 = (0, 0, 0), 001 = (1, 0, 0), 010 = (0, 1, 0), 011 = (1, 1, 0), 100 = (0, 0, 1), 101 = (1, 0, 1), 110 = (0, 1, 1) and 111 = (1, 1, 1). Then, construct the matrix representation of the 2³-field element ‘a’ in the following way. The first column is the vector corresponding to ‘a’ 001, the second column is the vector corresponding to ‘a’ 010, and the third column is the vector corresponding to ‘a’ * 100. Replace each element in the N by K encoder matrix over the 2ⁿ-field with the corresponding n by n matrix over the 2-field. So, the new encoder matrix has n x N rows and n x K columns with elements in the 2-field. Pick a fixed-size bit string length that aligns with the processor word size (usually 64 bits). Chunk the data into n such words. So, a data block has K chunks, each consisting of n words. And a code block has N chunks, each consisting of n words. A word in a code chunk is computed in the following way. Locate the corresponding row in the encoder matrix. For each column that has a 1, select the corresponding word in the data block. XOR all the selected words to obtain the code chunk word. Why XOR? Because addition in the 2-field is equivalent to a bitwise XOR.
There’s a lot to unpack above. Here’s all of it sketched out for a [3, 2] erasure code:

So, using a binary encoder matrix allows for encoding and decoding to proceed via blazing-fast XORs of word-length fragments of data/code.
How Can You Implement All Of This?
You now know how to keep your data safe by erasure coding it using an efficient, lossless implementation. It took a fair bit of math to get here. All of this theory can be translated into a working implementation relatively easily. I implemented a prototype in < 400 lines of Python code from scratch. Here’s a demo video of encoding an image of my puppy, Abby, using a [4, 2] erasure code and then decoding it back successfully from the first two shards:
There you have it. Go forth and erasure code. Use more math and spend less money to keep your data safe.








