Type I & Type II Errors
When statistical test results don’t correspond with reality
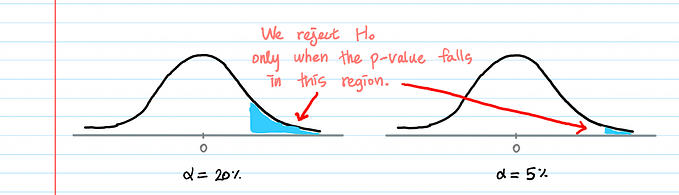
When performing statistical tests, the objective is to see whether some statement is significantly unlikely given the data. In more plain language, you are trying to determine if you believe a statement to be true or false. That statement is what is known as the null hypothesis (H₀) and the opposing statement is called the alternative hypothesis (H₁). The null hypothesis is, in a way, the default statement, as it is presumably true and it is the test’s job to challenge this. Much like in a court of law where you are “innocent until proven guilty,” unfortunately, sometimes innocent people are convicted when they shouldn’t have been, and guilty people are let free when they, in fact, did the crime. These two mistakes correspond to what are known in statistical testing as Type I and Type II errors, respectively.
In high school, my AP Statistics teacher taught us to remember that in a Type 2 error you fail 2 reject.
Type I Errors
A Type I error occurs when you reject the null hypothesis when you indeed should not have. In the aforementioned court example, a Type I error would be convicting an innocent person — the null hypothesis of innocence is rejected…