The Algorithm that gave my Program Artificial Intelligence to play Complex Board Games(Go)
If you are excited about the field of Machine Learning and Game Theory, this article is a must read. I’ll be looking at the basics of the Minimax algorithm with several improvements such as alpha-beta pruning. We will see how well it can play the ancient game of Go.
The expectation was high for this project. The goal of the project is simple, use Python without any external libraries to implement an artificially intelligent game playing agent. Go is an ancient board game believed to have been invented thousands of years ago in China. It has been the center of much AI research. You may be wondering: “why is this game so interesting?”
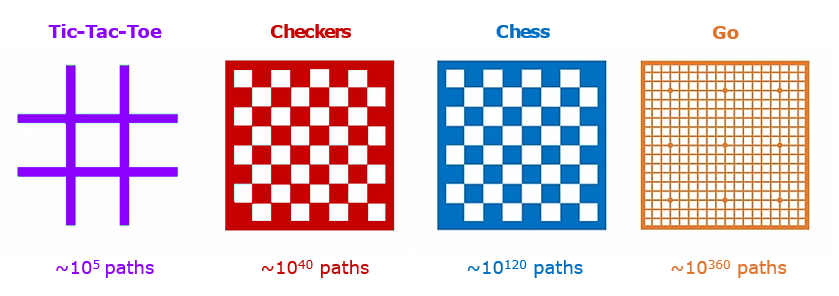
Go is a complex board game. It is played on a 19x19 board with more than 8 googol (8*10¹⁰⁰) possible legal board positions. If we mapped this out in a Game-Tree that translates to approximately 10³⁶⁰ possible sequence of moves. Games like checkers and chess only have 10⁴⁰ and 10¹²⁰ possible sequences of moves. To train a Deep Reinforcement Algorithm (i.e. the combination of Neural Networks + Q — Learning) will take time and space. I chose to use the Minimax algorithm with several optimization techniques to take on this challenge. In lieu of the 19x19 board, the game shall be played on a 5x5 board.
The Enemies
My AI agent will play against 5 different opponents with different algorithms/strategies. 50 games will be played against each opponent(25 as white, 25 as black)
- The Random Agent — Agent looks at the board for all possible legal moves, selects one at random.
- The Greedy Agent — Agent employs a greedy approach of looking for a move that will capture the most enemy stones.
- The Aggressive Agent — Agent looks at next two possible moves and picks the move that will capture the most enemy stones.
- The Game Playing Agent — Agent uses minimax with alpha beta pruning, evaluates based on which move will kill the most enemy stones.
Rules
To see a full definition of the rules, you may visit Sensei’s website. I will abbreviate the rules. The game will be evaluated with partial area scoring (every stone is worth 1 point). Two rules shall be observed: (1) Liberty and (2) KO.
Liberty — a stone must have a liberty (open adjacent square). Groups of stones may share a liberty. Stone’s without a liberty will be captured and removed from the board. KO — a board position cannot be immediately repeated. Black shall place the first stone. White will receive 2.5 points as compensation because of black’s inherent advantage.
The Result
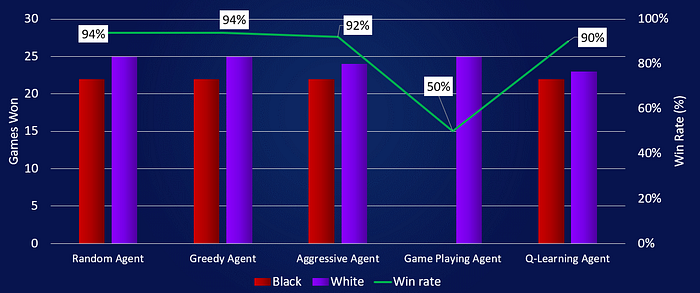
The agent was coded in Python, without the use of external libraries with implemented algorithms. On the chart above, I have tuned the agent’s play to be able to win against most opponents with a high success rate. I tested my agent in over 10,000 games and reached this performance. My agent used the minimax algorithm with several performance enhancements. I used: (1) alpha-beta pruning to reduce the size of the game tree and (2) external JSON file to store previously calculated moves.
How does it work?
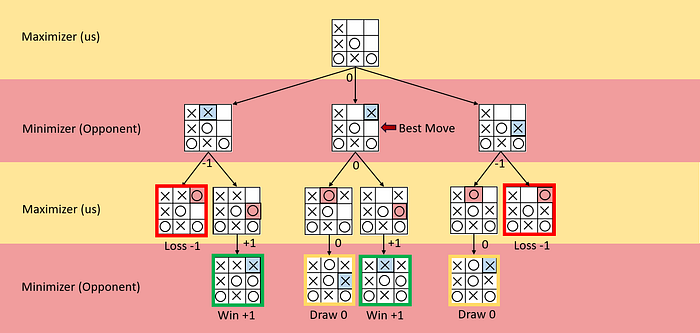
Minimax is an AI algorithm that works off the principal that we create an evaluation function that associates a board with a number. The algorithm will alternate between the maximizer (us) and the minimizer (opponent). A maximizer will always select the move that yields the maximum evaluation(utility). The minimizer selects the move that will minimize the maximizer’s utility. Above, I have created an illustration with Tic-tac-toe to demonstrate this principle. Alpha-beta pruning is an upgrade to the standard Minimax algorithm where we prune game tree branches that don’t improve our best potential score. Move ordering is very important in alpha beta pruning. Depending on the ordering, subsequent branches will not be investigated. With the pruning of some branches, we can increase the depth and width of our game tree. Below, you can see my pseudo code for my agent.

What criteria did I use to evaluate the board? First, I wanted to test the performance of a greedy strategy (picking the move that will kill the most enemy stones). To do this, I needed to develop 6 algorithms in this order: (1) find adjacent stones (2) find ally cluster (3) determine if a cluster has a liberty (4) determine if I can place a piece at a location and (5) find all possible valid moves and (6) remove all dead stones.
Algorithms
(1) Find all adjacent stones — Given a board position (i.e. 1,3) and a board. I returned a list of stones that were in adjacent positions (north, east, west, south). A simple for loop worked well here.
(2) Find Ally Cluster — Given a board position and a board. I returned the position of all allied stone. I implemented a Breadth-first search algorithm that searched from the current board position and used algorithm (1) to find child nodes.
(3) Determine if cluster has a liberty — Given a board position and a board, determine if a piece has a liberty. I used the current board position and found a set of board positions (i.e. (1,3), (2,3), (3,3)…) that share a liberty with the given board position (i.e. (1,3) using algorithm 2. With the list, I performed a linear search through the board and checked to see if the adjacent positions were empty.
(4) Determine if I can place a piece — Given a board position and a board, determine if it is possible to place a stone at the given board position. This one was tricky. I checked the following cases: is the position out of range (i.e. 6,6 is invalid), is the position taken by another stone, will this position have a liberty, and does this violate KO. Simple if/else checks can handle the case of the position being out of range and if the position is taken. Algorithm (3) solves the issue of if the current position has a liberty. Checking KO is simple. If we keep the past 3 board positions in memory. We can cross reference it to understand if we are violating the rule.
(5) Find all valid moves — Given a board and a player (black or white), determine all valid moves. This is simple to implement hence we can do a linear search and check the position with algorithm 4.
(6) Remove all dead stones — Given a board, determine what stones are captured/dead. This is simple, we can perform a linear search through all the positions on the board and determine if the current position is part of a cluster and has a liberty (algorithm 3).
At this point, I had a working greedy algorithm. But it wasn’t strong enough. I performed on par with algorithms with the same strategy. I wanted to develop a stronger evaluation function. Through research, I came across Erik van der Werf’s thesis, Solving Go on Small Boards. He recommended that we employ an algorithm used for looking at binary images. If we converted the board to a set of numbers 0 and 1's (0's represent empty/enemy positions, 1’s represent our positions) we could use Euler’s number to estimate how “connected” the board is. We know that groups of stones working together are more powerful than a lone stone. Maximizing liberties is also a good strategy when it comes to Go. We can use algorithm 3 to determine how many liberties each player has. Through research, it works well to discount edge moves (at the perimeter of the board).
Combining all of these together, we can create a strong evaluation function with many hyperparameters that we can tune. We know that if we are playing as black, we need to be more aggressive and really aim to kill enemy stones with less of a focus on board development (because of the 2.5 point Komi). If we are playing as white, we can put more emphasis on board development and less on killing enemy stones.
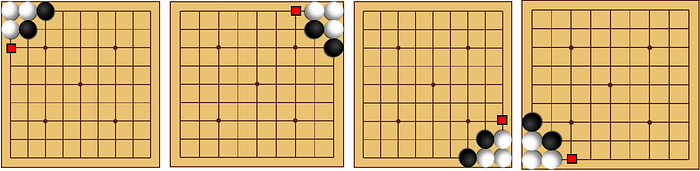
I wanted to make the decisions even faster. During the process of minimax, we are computing the same board position over and over. Using dynamic programming, we can store previously calculated moves into a table. After each turn, I chose to dump the table into a JSON file for future games. This speed up the algorithm by a lot. Games went from 2000 seconds of computation to 400–600 seconds. That is a speed increase of up to 500%! I did not do this, but we could take advantage of symmetry. Below, I have depicted 4 boards that have the same solution; a 90 degree rotation should not affect our result. For a single board, we could store its result and the result for each equivalent board in our table.
Conclusion
This project shows that with some knowledge of the game you are playing, we can teach an AI to perceive its environment and select moves based on some set evaluation criteria. Without any training whatsoever, the AI was able to begin playing games and producing results. Against most enemies it performed well. From here, we could improve our AI by splitting the AI’s decision into two brains (one for when the AI is playing as black and one for when the AI is playing as white). We could try using other algorithms such as Deep Q-learning, where we can write our own neural network implementation from scratch and develop optimal policy based on rewards.
I have written an entire guide to creating a Neural Network from scratch:
Implementing a Multi Layer Perceptron Neural Network in Python
