More on Anomaly Detection with Autoencoders: Measuring Sequence Abnormality with Keras
Use the Keras framework to design a simple autoencoder that can learn patterns of string sequences and detect the faulty ones.
A few months ago I posted a story showing how to use an autoencoder (a certain type or architecture of a NN that is mostly used for dimensionality reduction and image compression) to efficiently detect an anomalous or faulty string sequence in a large set of sequences. Given a list of sequences following a certain pattern or format (e.g. ‘AB121E’, ‘AB323’, ‘DN176’), I showed how we can design a network that will learn these patterns or formats and will be able to detect cases in which a sequence was not formatted properly. In this story, I want to show a more “advanced” use case, or how we can use the same methodology to address a somewhat more complicated problem. Sometimes, the question we want to answer is not whether or not a certain sequence is anomalous or an outlier, but how anomalous or abnormal a given sequence is comparing to other sequences. Suppose, for example, that it is pretty normal to have some anomalous sequences per hour in our data stream, but we need to find a way to evaluate how normal or abnormal a certain hour is comparing to the last one. We can calculate the average level of abnormality that we saw every hour but how do we go about something like this?
I won’t delve into the theory of autoencoders and how they work (there is quite a bit of good and accessible reading material out there — I have mentioned a few below), but the basic idea, in short, is that an autoencoder is a form of network that learns compressed representations of its input data and tries to reconstruct it. By learning how to reconstruct a sequence from its compressed representation, a well-trained autoencoder can be said to learn the “dominant rules” that govern its formatting (I should admit that although this analogy is helpful for some folks, not everyone finds appealing this idea of learning compressed representation as learning the formatting rules). Therefore, we can use such autoencoder to estimate how the formatting or pattern of a certain sequence differs or diverges from the others.
Following the “code first” approach, I will immediately delve into the code and proceed in 3 main steps:
- Prepare the sequences for deep learning — tokenize , pad, and vactorize (it depends on the problem at hand, but i do not believe that this simple problem required use of embeddings — either learned or pre-learned).
- Create and train an autoenoder
- Predict and score
1. Sequence Preparation
1.1 Tokenizing
So we have a pretty large data set of about 250K sequences (the success of the methodology described here heavily depends on having a large sample). Sequences generally look like this:

As you can see, most sequences are made of 4 components (or more), and seem to follow a certain pattern or format, though we don’t know it.
The first task we need to do is to tokenize the sequences and create numerical representations for each component (or word) in the sequence — i.e. turn [‘AB’ ,‘C1’ ,‘D5'] into [1,7,6]. To do this I use Keras’ Tokenizer class which takes care of most of the low level steps involved in tokenization.
I define a vocabulary of size 750 — which means that the Tokenizer will only create representation for the 750 most frequent tokens in the data set.
After the tokenizer was fit() on our data set, we can use the tokenizer’s property word_index to get a dictionary object which can be used to examine the numerical representations that were assigned to each part.
We complete the tokenization stage by calling the tokenizer’s method texts_to_sequences() on our sequences in order to get an array with numerical representations of all the sequences in our set.

We now have a set of tokenized sequences ([1,3,31,22]) or a set of numerical representations of our original set ([DF, 36, FR, GX567]).
1.2 Padding
The next step we need to take concerns the length of the sequences we want to base our analysis on. In the best scenario, all sequences will be of the same length, but sometimes this is not the case. This question is important as it bears on the features that our model will use. Because all sequences need to be in the same length (you will later see why), short sequences are typically padded with zeros to match the length of the longer ones. So, if we decide that the number features we want our model to learn is 6 then we need to “pad” this sequence with zeros [1,3,31,22] and transform it into this sequence [1,3,31,22,0,0].
In our case, for example, the vast majority of the sequences have 4 components but some don’t.

The mean length of our sequences is indeed 4 but we see that there are some “outliers” that have much more. However, because most sequences have just 4 components and because unnecessary padding might impact the performance of our model, its better we stick with 4, so that all we have to do is pad the sequences that have less than 4 components.
We do this using this one-liner:
MAX_FEAT_LEN = 4
pad_seqs = pad_sequences(seqs, maxlen=MAX_FEAT_LEN, padding='post', truncating='post')1.3 Vectorizing
Our final, and most important, step is to vectorize each sequence. By vectorizing our sequences we transform (or flatten) sequences like this: 1,4,31,22
into this:

What you see here is a vector of size 750 (which is our vocabulary size) that consists of 746 zeros and 4 ones, while the location or index of each ‘1’ representד its numerical value. In other words, the sequence 1,4,31,22 will be represented in vector v as:
v[1] = 1
v[4] = 1
v[31] = 1
v[22] = 1This can be implemented rather easily using this method:
Now our sequences are ready to be learned!
2. Create and Train an Autoencoder
I won’t get too much into the details here as I believe that the code is pretty much straightforward and self explanatory if one is somewhat versed in DL and Keras. In short, however, autoencoders are typically created by connecting an encoding layer that compresses or squeezes the input into a lower dimensional layer thus creating a sort of a “bottleneck”, and a decoding layer that learns to reconstruct the input from the compressed representation of the input data.
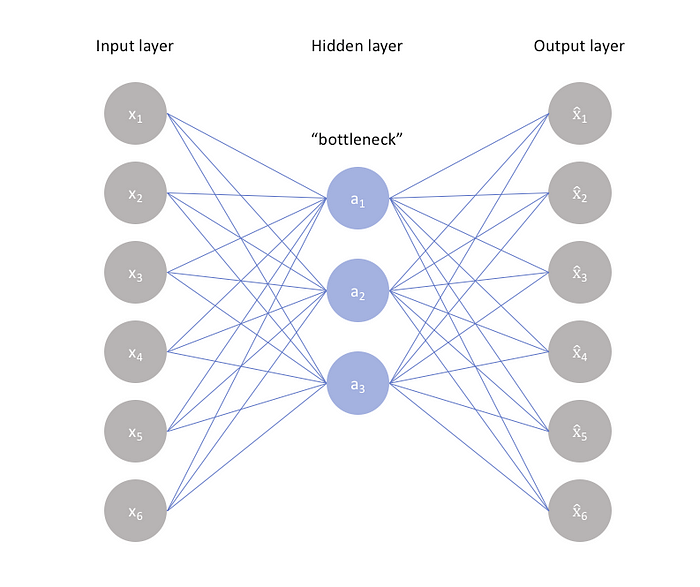
Autoencoders can obviously be designed in more than one way according to the problem at hand. I chose to use a very simple example (mostly due to the nature of the data and its relative in-complexity) that can be implemented quite simply using Keras as follows:

This is usually not required, but in case you would like to closely follow and watch the performance of your model and save it ( like I do) then this can be helpful (otherwise you can just call the autoencoder compile() and fit() method.
Assuming that the model performed good enough we can now load it and move on to examine and score our sequences:
autoencoder = load_model('model_bin.h5')3. Predict and Score
So now we got to the fun part. We have an autoencoder that receives a string sequence as an input (after it has been tokenized, padded, and vectorized) and outputs a reconstruction of the same sequence. But this output is not really interesting — if our autoencoder works properly it will simply output something very similar to the input sequence we gave it. What is interesting about the output of the autoencoder is how different the output and input sequence are from each other. Assuming that our autoencoder is well trained then if the input sequence is well formatted or if it follows the same patterns that the autoencoder has learned from the training data, then the output sequence will be identical or similar. Correspondingly, if the input sequence does not follow the patterns that the autoencoder has learned then the output sequence will be much less similar to the input sequence.
Therefore, if we want to examine whether or to what extent some sequence follows the patterns that the autoencoder has learned from the training data, then we need to measure the difference (or the error) generated by autoencoder’s prediction or from the sequence it outputs. But how do we do that?
Let me propose one possible approach. After tokenizing, padding, and vectorizing, each sequence is basically a vector of zeros with ‘1’ at the index location of each numeric token — so that [1,3] will be represented as [0,1,0,1,0,0] in a 6 chars vocabulary vector. If our autoencoder will receive this input and will output the sequence [0,1,0,0,1,0], which is represents the sequence [1,4], then we have an error. What we would like to achieve is to find a way to measure this or measure the degree to which the two sequences are different. One of the most efficient ways to do this is simply to get the mean square error of each output sequence by (1) subtracting the input and output to count the errors; (2) square the result (to cancel any negative); (3) take the mean of errors as a measure of how “faulty” an output sequence is.
This piece of code will make this clearer.

Here we have 3 input sequences and 3 output sequences. While the first output sequence has no mistakes at all, the second output sequence has one mistake and the third has two. That is clear when we look at the output of subtracting them:
Result of subtracting the vectors:
[[ 0 0 0 0 0]
[-1 0 0 0 0]
[ 0 0 -1 -1 0]]When we square the error and take the mean of every sequence then we get a measure of the faultiness or degree in which it diverges from the input sequence.
Errors:
[0. 0.2 0.4]So all we need to do in order to implement this in our use case is to get the output sequences from the autoencoder by calling predict on the input sequence and then square the num of errors and take the mean.
Now, each sequence has a certain score that represents its degree of difference from the input sequence and we can use this to measure how well this sequence follows the patterns learned by our autoencoder. Yet this score, in itself, is not very helpful or tell us anything (in fact it would a mistake to take this number into account in itself regardless of the size of the vocabulary at hand). One way that we can use this is by measuring the mean value of error in our data set — np.quantile(mse, 0.5) and then treat each sequence above this threshold as more abnormal than others; and sequences with measured error above the 75th percentile as much more abnormal, and so on. This will allow us to score a sequence according to the its degree of divergence from the pattern learned by the autoencoder.

However, it would be more accurate and efficient to do the opposite — being able to know what is the percentile to which some sequence corresponds in order to get its anomaly score. This is what the following method essentially does: after preparing the string, it uses the autoencoder’s predict() method, get the error term associated with the output sequence and get the percentile rank of the error value which can give us a more accurate representation of its conformity to the learned pattern.
As you can below, the sequence ‘9 ER 223 ABCDSED’ has a percentile rank of 73.8 which means that it is relatively abnormal considering the number of prediction mistakes that the autoencoder has made with respect to it. This may mean that it diverges considerably from the patterns that the other sequences follow as learned by the autoencoder.
score, rank = get_sequence_anomaly_rank('9 ER 223 ABCDSED')print(f'Anomaly Score:{score}, Percentile Rank:{rank}')==> Anomaly Score:[0.00346862], Percentile Rank:73.85446487442933
It is now simple to measure the degree of abnormality of certain sequences as well as groups of sequences. In order to evaluate the degree of abnormality of a certain group all we need to do is calculate the weighted mean of the errors that the members of this group generate.
I hope this was helpful!
Example notebook can be found here
Some links about autoencoders:

