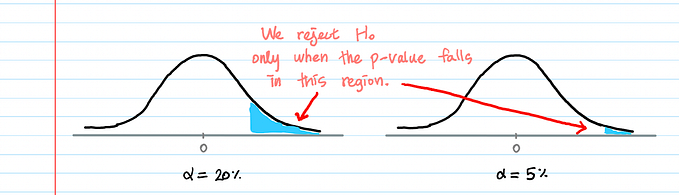
Mean or median? Choose based on the decision, not the distribution
Even for skewed data, the mean sometimes leads to better decisions
When I interview data science applicants, one of my favorite questions is, “When is it better to use the mean instead of a median?”
Not only does this question help me assess a candidate’s statistical foundation, but it also gives me a glimpse into how they approach problems. Do they emphasize the nature of the data or the decision?
Most candidates will answer with something like this:
“The mean is typically better when the data follow a symmetric distribution. When the data are skewed, the median is more useful because the mean will be distorted by outliers.”
This answer captures the conventional wisdom I learned in statistics courses. It focuses on the nature of the data and does not consider the goals of the analysis.
Decision analysis courses taught me a different approach to this problem. Rather than focusing on the nature of the data, decision analysis leads us to focus on our goals.
In reality, there are many applications in which the mean is a more useful measure than the median, even with skewed data.
Let’s start with three classic examples involving skewed data in which either the mean or the median fails spectacularly.
Example 1: Monetary lotteries
Let’s say that you can choose to play one of the following games of chance:
Game A:
- A 1/3 chance of winning $1
- A 1/3 chance of winning $2
- A 1/3 chance of winning $3
Game B:
- A 1/3 chance of winning $1
- A 1/3 chance of winning $1.90
- A 1/3 chance of winning $1,000,000
Which one would you pick?
Most people would choose to play Game B even though it has a lower median ($1.90 vs. $2.00). In this case, the use of the mean makes a lot more sense, even though the distribution is skewed.
The argument for the median doesn’t make sense here:
“I should base my decision on a measure that isn’t influenced by the fact that I have a 1 in 3 chance of becoming a millionaire with Game B.”
The 1/3 chance of $1,000,000 is an extreme value, but it’s part of the distribution and relevant for decision-making.
Example 2: Bill Gates walks into a bar
A common joke goes something like this:
“Bill Gates walks into a bar, and everyone inside becomes a millionaire, on average.”
This joke highlights how the mean can be misleading. Without context, one might think that the bar is full of millionaires when it might consist of zero millionaires. In this case, the median gives a result that most people would find more intuitive.
An essential feature of this example is that it is about data communication and not decision-making. This example is the only one that does not involve a clear decision.
The point about data communication is undoubtedly a valid one; there is a good reason why the researchers use the median when reporting household incomes. The median often gives a better sense of what a “typical” value is, which helps provide an intuition about the dataset.
The measure that gives the most intuitive sense of a “typical” value is not necessarily the measure that leads to the optimal decision-making policy.
Example 3: A company considering an expansion
A company is considering an expansion. The expansion would involve hiring 300 new employees, so the company needs to estimate the total cost of the initiative.
Salaries, like incomes, tend to be skewed right. We can expect that the mean salary of the new jobs would be larger than the median.
An analyst in the company decides to use the median because the distribution of salaries is skewed right. They multiply the median by 300 to estimate the total cost of hiring the new employees.
It turns out that the actual cost was much higher than their estimate. Why? Because they should have used the mean.
In this case, the company was interested in a total. The mean has a direct relationship with the total (total = mean x N), but the median does not.
In general, when the purpose of the analysis is to estimate a population total, the mean is a more useful measure than the median, regardless of the shape of the distribution.
A simulation of two competing companies
One of the best ways to evaluate the efficacy of a statistical approach is to perform a Monte Carlo simulation on synthetic data.
So, let’s simulate a company that makes decisions based on the mean competing against a company that makes decisions based on the median.
A *relatively* simple business decision we can simulate is an A/B test. In an A/B test, a company faces the decision of releasing two different versions (variants) of a product — A and B.
For simplicity, we will simulate this as a “winner take all” test, meaning that the companies choose the variant that appears better from the test without calculating statistical significance. This approach is reasonable when there is no control group, and the business question is relatively low risk.
Before releasing variant A or B to the entire customer base, the company tests variant A with a sample of customers and variant B with a different sample of customers.
Based on the performance of variants A and B in the test, the company chooses to release either variant A or variant B to the entire customer base.
Here is a summary of the setup. On each simulation:
- We will randomly generate two skewed distributions. These distributions represent the true distributions for the revenue per user for variants A and B.
- To decide which variant to release, the companies will analyze a dataset consisting of 1,000 draws from variant A’s distribution and 1,000 draws from variant B’s distribution. These draws comprise the “test dataset.”
- To isolate the impact of the decision-making approach, both companies analyze the same A/B test dataset.
- Each company will choose either A or B based on the test dataset.
- After choosing a variant, each company launches its preferred variant “at scale” to its entire customer base. We will simulate this step by generating 100,000 draws from each company’s chosen distribution. These draws represent the revenue received from each company’s 100,000 customers.
- The business objective is to maximize the total revenue, so we will evaluate each company’s decision-making policy based on each company's total revenue when it releases its preferred variant at scale.
Now let’s get into the Python implementation. The full implementation is available on GitHub. I encourage readers to experiment with it to understand how different decision-making frameworks lead to different business outcomes.
First, we need to write a function that generates random skewed distribution. I chose log-normal distributions as they are a common model for skewed data.
Recall that if a variable x has a log-normal distribution, log(x) has a normal distribution. I find it intuitive to characterize the parameters of the log-normal distribution based on the mean (mu) and the standard deviation (sigma) of the underlying normal distribution.
In this function, we randomly draw mu from a uniform distribution between 0 and 0.5 and draw sigma from a uniform distribution between 1 and 1.5:
This function generates distributions like those shown below:
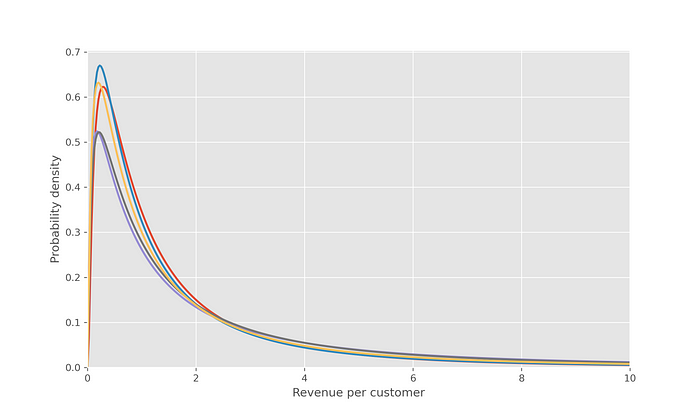
In each simulation, the companies will be presented with two of these distributions, and they will need to choose one based on a random sample of 1,000 draws from each distribution.
Here is an example of what the test datasets look like:

Looking at these datasets, the two companies come to different conclusions about how they should make their decision:
- The Median Maxers notice that the distribution is very skewed. In fact, it looks like some of the data points might be outliers. To diminish the impact of the outliers, they choose the distribution whose test dataset has the higher median.
- The Mean Maxers realize that the underlying goal is to maximize total revenue, so they choose the distribution whose test dataset has a higher mean.
We can represent the decision-making policies of the two companies with the following functions:
After running 5,000 simulations, the revenue distributions for the two companies are shown below.

Although the total revenue varies across simulations for both companies, it is clear that the distribution of revenue for the Mean Maxers is noticeably higher.
We can also look at a barplot to answer the question: What percentage of the time did the Mean Maxers outperform the Median Maxers?

The Mean Maxers outperformed the Median Maxers in about 60% of the simulations.
This result is interesting. Intuitively, it would seem that the two companies should often come to the same conclusion since the distribution with the higher mean should often have the higher median.
Based on the log-normal parameters we used, the companies chose the same variant in about 70% of simulations. When the companies choose the same variant, there is a 50% chance that either company will outperform the other.
However, when the companies chose different variants, the Mean Maxers outperformed the Median Maxers in about 86% of the simulations.
These numbers are dependent on the exact simulation setup we used, but the key takeaway is that this represents a fairly common business situation in which the goal is to maximize a total. With this goal, making decisions based on the median rather than the mean leads to a strategic disadvantage.
When should we use the median (or, more generally, a quantile)?
To be clear, I am not arguing that the median is never helpful. Sometimes the median aligns with the goals of the analysis.
There are applications in which the median (or a quantile) has advantages over the mean. Here are a few:
- Data storytelling. The median is often more helpful for reporting skewed data when there is no clear decision at hand. It gives a more intuitive sense of a “typical” value from a distribution. However, there is almost always a decision at hand for data scientists working for a company.
- Sometimes a question is directly answered by the median. If we need to know whether a given salary is higher than half of the salaries in the department, we need the median.
- When we care about ensuring a certain level of service. For example, when I work with fire departments, they care about providing a certain response time with a high probability. As a result, they often use the 90th percentile response time to evaluate their performance. If they used an average response time, they could compensate for long response times with very short ones, which misaligns with public safety goals.
- When we are incentivized to minimize the absolute error of a prediction. As discussed in this paper, the median of a distribution is the value that minimizes the mean absolute error.
What about log transforms?
A common approach to handling skewed data is to use a data transformation, such as taking the logarithm. These transformations are helpful in many applications; they can alleviate right-skew, force the data to be positive, and improve the performance of predictive models.
However, we also need to be careful that we are not using them in a way that unintentionally changes the decision-making policy.
Which of the two following options would you prefer:
- Option 1: A $10 bill and a $1 bill
- Option 2: Two $5 bills
Most people would choose Option 1, because $10 + $1 is greater than $5 + $5. If you take a log transform before taking the sum, you will prefer Option 2 because $5 x $5 is greater than $10 x $1. The log transform changed the decision-making policy.
This change is not necessarily bad. It makes sense to base decisions on a product instead of a sum in some contexts.
The problem occurs when our effort to make the statistics easier unintentionally leads our stakeholders into a suboptimal strategy.
In the simulation from the previous section, I considered adding a third company, the Log Transformers, who would take the logarithm of the test dataset before taking the mean. They would then choose the variant with a greater mean on a log scale. This policy is equivalent to selecting the distribution with the higher geometric mean.
The median is equal to the geometric mean for log-normal distributions, so the Log Transformers would have a nearly identical strategy to the Median Maxers. Their strategy would also be inferior to that of the Mean Maxers.
What about outliers?
When the optimal decision-making policy suggests that we should use a mean over a median, we need to be careful about outliers because they can skew the mean.
But the answer is not to replace the mean with a measure that leads to sub-optimal decision-making.
Instead, we should understand why the outliers are in the dataset in the first place.
Are they the result of a measurement error? If so, we should consider excluding them from the analysis. If the outliers are accurate measurements of reality, we need to use sound judgment.
The outliers could be the result of a fluke. For example, on an e-commerce website, a small fraction of the customers could be businesses that make unusually large orders. If you are running an A/B test and a test group includes a user like this, it could skew the results in an undesirable way.
Depending on the situation, other approaches such as winsorized means could be helpful. There is no universal solution here. The best advice is to focus on the goals of the analysis, develop domain knowledge to understand the causes of outliers, and then use good judgment from there.
When dealing with outliers, focus on understanding why they exist in the first place. After that, ask yourself if they are a meaningful part of the distribution.
Should we use summary statistics at all?
Some hold that summary statistics are inherently misleading in some situations, and we should focus on the “entire distribution” instead.
This notion has some merit. Looking at the entire distribution can reveal insights that standard summary statistics fail to capture.
For example, looking at the distribution in an A/B test can reveal heterogeneous effects — meaning that a treatment may have a different effect on some users than others.
However, our goal is usually to translate data into a decision, which requires summarizing distributions in an actionable way.
A quantative decision-making framework requires summarizing a distribution with a single number that quantifies how much it aligns with the decision-maker’s preferences.
Without this, we cannot quantify whether one distribution is better than another. Decision analysis helps solve this problem; one of its central aims is to capture preferences and distributions in a single number— the utility of the action.
So yes, we need summary statistics. We should explain what’s driving the summary statistics, but it is essential that we know how to summarize a distribution in a way that captures the preferences of the decision-maker.
It’s also important to note that there are many other ways to summarize distributions, such as harmonic means, geometric means, and certain equivalents. All of them are useful in some situations depending on the nature of the decision.
Conclusions
Now that we have explored the question in-depth, we can present a more thoughtful answer to “when is it better to use a mean instead of a median?”
Here is how I would answer the question:
The choice to use a mean or a median should be primarily driven by the goals of the analysis. When the underlying business decision depends on a total (e.g. total revenue or total sales), the mean is usually the better metric because, unlike the median, it has a direct relationship with the total. Means are sensitive to extreme values, so care should be taken to ensure that they are calculated on clean, meaningful datasets. When the distribution is skewed, the median can provide a more intuitive sense of a “typical” value, but this does not necessarily mean that it is the basis of the optimal decision-making policy.
This topic also highlights the need for data scientists to incorporate topics from decision analysis into their study diet alongside statistics, machine learning, and programming.
Thank you for reading this post. If you are interested in more decision analysis and statistics content, follow me on Medium or connect on LinkedIn.
Recommended resources:
- The Foundations of Decision Analysis by Ronald A. Howard. This book provides an excellent overview of the core concepts of decision analysis. These concepts have been instrumental in my growth as a data scientist.
- Mean, Median and Mode from a Decision Perspective by Melinda Miller Holt and Stephen M. Scariano. This paper outlines the mathematical conditions that make the mean, median, or mode the optimal measure for decision-making. Some of the described incentive structures are uncommon in practice, but this paper provides an interesting mathematical framework for choosing a summary statistic.
- Can You Solve This Archery Riddle? by FiveThirtyEight (YouTube video). This riddle outlines a situation in which the mean is not the ideal measure for decision-making. Some point to this riddle as an example of the mean not being useful because the distribution is skewed. I’d argue instead that it’s about the goals of the analysis. The objective is to maximize the win probability, which is different from maximizing the expected total score.