You're reading for free via Soner Yıldırım's Friend Link. Become a member to access the best of Medium.
Logistic Regression — Explained
Detailed theoretical explanation and scikit-learn example
Logistic regression is a supervised learning algorithm which is mostly used for binary classification problems. Although “regression” contradicts with “classification”, the focus here is on the word “logistic” referring to logistic function which does the classification task in this algorithm. Logistic regression is a simple yet very effective classification algorithm so it is commonly used for many binary classification tasks. Customer churn, spam email, website or ad click predictions are some examples of the areas where logistic regression offers a powerful solution.
The basis of logistic regression is the logistic function, also called the sigmoid function, which takes in any real valued number and maps it to a value between 0 and 1.

Logistic regression model takes a linear equation as input and use logistic function and log odds to perform a binary classification task. Before going in detail on logistic regression, it is better to review some concepts in the scope probability.
Probability
Probability measures the likelihood of an event to occur. For example, if we say “there is a 90% chance that this email is spam”:

Odds is the ratio of the probabilities of positive class and negative class.

Log odds is the logarithm of odds.

All these concepts essentially represent the same measure but in different ways. In the case of logistic regression, log odds is used. We will see the reason why log odds is preferred in logistic regression algorithm.
Probability of 0,5 means that there is an equal chance for the email to be spam or not spam. Please note that the log odds of probability 0,5 is 0. We will use that.
Let’s go back to the sigmoid function and show it in a different way:

Taking the natural log of both sides:

In equation (1), instead of x, we can use a linear equation z:

Then equation (1) becomes:

Assume y is the probability of positive class. If z is 0, then y is 0,5. For positive values of z, y is higher than 0,5 and for negative values of z, y is less than 0,5. If the probability of positive class is more than 0,5 (i.e. more than 50% chance), we can predict the outcome as a positive class (1). Otherwise, the outcome is a negative class (0).
Note: In binary classification, there are many ways to represent two classes such as positive/negative, 1/0, True/False.
The table below shows some values of z with corresponding y (probability) values. All real numbers are mapped between 0 and 1.

If we plot this function, we will get the famous s shaped graph of logistic regression:

The classification problem comes down to solving a linear equation:

Parameters of the function are determined in training phase with maximum-likelihood estimation algorithm. Then, for any given values of independent variables (x1, … xn), the probability of positive class can be calculated.
We can use the calculated probability ‘as is’. For example, the output can be a probability that the email is spam is 95% or the probability that customer will click on this ad is 70%. However, in most cases, probabilities are used to classify data points. If the probability is greater than 50%, the prediction is positive class (1). Otherwise, the prediction is negative class (0).
Everything seems ok up until now except for one issue. It is not always desired to choose positive class for all probability values higher than 50%. Regarding the spam email case, we have to be almost sure in order to classify an email as spam. Since emails detected as spam directly go to spam folder, we do not want the user to miss important emails. Emails are not classified as spam unless we are almost sure. On the other hand, when classification in a health-related issue requires us to be much more sensitive. Even if we are a little suspicious that a cell is malignant, we do not want to miss it. So the value that serves as a threshold between positive and negative class is problem-dependent. Good thing is that logistic regression allows us to adjust this threshold value.
If we set a high threshold (i.e. 95%), almost all the predictions we made as positive will be correct. However, we will miss some of the positive class and label them as negative.
If we set a low threshold (i.e. 30%), we will predict almost all the positive classes correctly. However, we will classify some of the negative classes as positive.
Both of these cases will affect the accuracy of our model. The simplest way to measure accuracy is:

However, this is usually not enough to evaluate classification models. In some binary classification tasks, there is an imbalance between positive and negative classes. Think about classifying tumors as malignant and benign. Most of the target values (tumors) in the dataset will be 0 (benign) because malignant tumors are very rare compared to benign ones. A typical set would include more than 90% benign (0) class. So if the model predicts all the examples as 0 without making any calculation, the accuracy is more than 90%. It sounds good but is useless in this case. Therefore, we need other measures to evaluate classification models. These measures are precision and recall.
Precision and Recall
First, we need to define some terms:
True positive: Correctly predict positive (1) class
False positive: Predict negative (0) class as positive
True negative: Correctly predict negative (0) class
False negative: Predict positive class (0) as negative

It is desired to make a prediction that is either TP or TN so the models aim to maximize TP and TN values.
Precision measures how good our model is when the prediction is positive.

Recall measures how good our model is at correctly predicting positive classes.

We cannot try to maximize both precision and recall because there is a trade-off between them. The figures below clearly explain the trade-off:
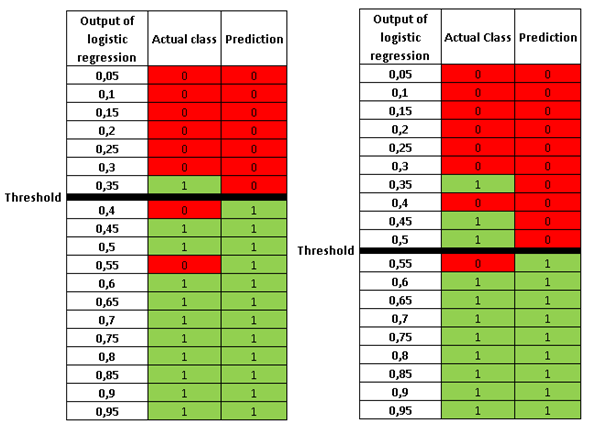
In both tables, there are 8 negative (0) classes and 11 positive (1) classes. The prediction of the model and hence precision and recall change according to the threshold values. The precision and recall values are calculated as below:

Increasing precision decreases recall and vice versa. You can aim to maximize precision or recall depending on the task. For an email spam detection model, we try to maximize precision because we want to be correct when an email is detected as spam. We do not want to label a normal email as spam (i.e. false positive). If false positive is low, then precision is high.
There is another measure that combines precision and recall into a single numbet: F1_score. It is the weighted average of precision and recall and calculated as:
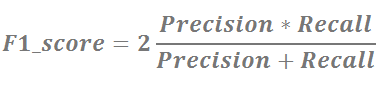
F1_score is a more useful measure than accuracy for problems with uneven class distribution because it takes into account both false positive and false negatives.
Note: L2 regularization is used in logistic regression models by default (like ridge regression). The regularization is controlled by C parameter. Because of this regularization, it is important to normalize features (independent variables) in a logistic regression model.
Scikit-learn Implementation
I will use one of the datasets available under datasets module of scikit-learn. I will import the dataset and dependencies:

Then load the dataset and divide into train and test sets:

Create a logistic regression object and fit train data to it.

Then predict the target variable in test dataset:

Scikit-learn provides classification_report function to calculate precision, recall and f1-score at the same time. It also shows the number of positive and negative classes in the support column.

It is worth noting that data preparation, model creation and evaluation in real life projects are extremely complicated and time-consuming compared to this very simple example. I just wanted to show you the steps of model creation. In real-life cases, most of your time will be spent on data cleaning and preparation (assuming data collection is done by someone else). You will also need to spend a good amount of time on the accuracy of your model with hyperparameter tuning and re-evaluating many times.
Thank you for reading. Please let me know if you have any feedback.
My other posts on machine learning algorithms
- Naive Bayes Classifier — Explained
- Support Vector Machine — Explained
- Decision Trees and Random Forests — Explained
- Gradient Boosted Decision Trees — Explained