Notes from Industry, Making Sense of Big Data
How to Address Functional Challenges of a Demand-Forecasting Engine
Designing a comprehensive forecast solution that can be deployed into a production pipeline at scale.
Demand forecasting in retail industry is an age-old problem and different solutions are already devised to overcome a lot of challenges. But the problem seems to be ever existing and not all business stakeholders are happy with the way their current demand forecast engines are functional. There can be a plethora of challenges starting from incomplete time-series, data cardinality, stock outs, discontinuation of products, new product launch, new store launch, structural shift from in-store to delivery channel, occurrences of catastrophic events like covid that change the entire dynamics of customer perception and their purchase behaviour, effect of cannibalisation and halo, scaling up an efficient engine to generate forecast for millions of SKUs, model management complexities, integration of business rules in final decision engine etc. There are means through which some of these concerns can be handled elegantly but that requires lot of customisation during selection of modelling framework. In the article we are going to cover these customisations and how to design a comprehensive forecast solution that can be deployed into a production pipeline at scale.
To begin with, we will start with an important concept of mixed effect model (often called as linear mixed effect model — LME). Before going into the realm of that, it’s important to understand the concept of “pooling” and “no pooling”.
Suppose you are to forecast demand of 10 products for next 4 weeks given a history 208 weeks (i.e., 4 years of data). This translates into 208*10 i.e., 2080 row items that we have as part of the training data. Now truly speaking, demand of one product can have an associated impact on other products as well. It violates one of the major assumptions of independence and identical distribution (i.i.d.). When we assemble the entire series 2080 row items and build a single model to capture the demand (This is known as “Pooling”), it usually generates over-estimated parameters and often produce incorrect estimates due to structural incorrectness of the data. For non-uniform/ incomplete time-series, it often generates estimates that are biased towards the time series having more data points. In case of no-pooling, we usually treat each series individually and forecast their demand (this is known as no-pooling). For no-pooling models, inter-product variability is often ignored because each product is treated differently. This results in an incorrect estimation of the slope. To overcome the limitations of these two methods, we often use “partial pooling method” also called as mixed effect model. Based on the pooling variables or random effects, estimation of coefficients will vary. To give an example, consider the following form.

It implies that intercept and price coefficients will vary by product groups Similarly,

implies that price elasticities of cross products won’t vary by product groups. Hence these are called as fixed effects in the model. Selection of fixed and random effects are not discussed as part of the current blog but it is recommended to include the variables of greatest interest as random slopes across grouping variables. But one point to note here is that partial pooling can handle incomplete time series and data cardinality to some extent.
How to control decisions on some of your key variables?
Demand forecasting is often associated with other business decision making processes like price recommendation, discount strategies, inventory planning etc. Hence these exogenous variables will come as features in the demand model. So, it’s important to know how to control these variables in presence of other features. Business often put lot of restrictions on how these key features can vary and its impact should have a governance mechanism and should not be uncontrollable.
Can we take them out and model separately?
A standard additive demand model looks like the following:

Now let us decompose the demand series into trend and seasonality. Hence the residuals can be considered as follows:

Here Residual1 is also known as decomposed demand. Now let’s try to develop a mix effect model with only price as the key feature. So the model equation would look like the following:

Please note that the above residual model is important only to estimate the elasticity. Now that we have price elasticity for both self and cross products, let’s look at the rest of the features.


So Residual2 will majorly determine the accuracy of the demand forecast keeping the price controllability aside. Now to calculate the elasticity, we will add everything back together in a single equation like the following:
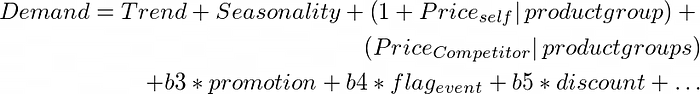
One major advantage of this approach is to ensure that price impact is controllable and to improve the demand forecast accuracy, plethora of sophistication can be experimented on Residual2 model keeping price explain-ability intact.
How to handle stock outs?
Stock outs are extremely common phenomena when it comes to retail and CPG industry. As a result of stock outs, we often tend to see a discontinuity in the time series which, unless taken with due importance, can portray a completely opposite story. There are couple of ways we can deal with this scenario but the simplest way to do are the followings:
1. Create flags for the days of stock outs — In case we know the information about the stock outs, we should be able to identify the weeks/days on which certain products were out of stock. Creating a flag against those specific dates/weeks should be able to capture the dip in sales. But in case we don’t have any specific information about the same, we would still be able to do that as part of the exploration. If there are certain instances where demand dips down to 0 abruptly and then picks up again after a few days/weeks to its fullest capacity, that can possibly indicate stock out phenomena.
2. Imputation for stock outs — There are cases where we don’t want to create additional variable through flags but would like to adjust the demand itself. We can achieve this through imputation mechanism. Cases where we identify stock outs, we can replace them with absolute numbers (like max/mean/median) or moving average (with 2-weeks/3-weeks average).
Effect of Cross products and how to model them?
In any demand forecasting problem in retail scenarios, one of the major challenges come during estimation of cross impact of other products from same category/ different categories on the self-product. At times, because of numerous product categories for large retailers, these cross impacts can trouble a lot. But with judicious approach, these problems can be solved elegantly. So let’s identify the steps which we can follow to converge on the methodology.
Step 1: Selection of cross products
The first step before measuring the impact of cross product is to identify them. Often these are identified by business teams based on product knowledge and customer behaviour. But we can identify that from data too. A simple association rule mining or market basket analysis can indicate the list of items that are bought together by customers. Now this list can be sparse at times which potentially can cause an overfitted model if not considered cautiously. Hence, it’s important to filter out the list based on sales contribution. Usually, long tail products is a common phenomenon for most of the retailers and a prudent filtering can cut down the long tail keeping only relevant product as part of the scope.
Step 2: Measuring the impact
If the model is multiplicative in nature i.e., if the demand function takes a functional form of the following –

In such cases, coefficient corresponding to price of cross items can directly be translated to elasticity. This means with 1 unit change in price of cross product, there will be b2 unit change in demand.
In other cases where the model takes a semi-log functional form like the following –

Coefficient corresponding to cross product price can be interpreted as unit change in price will result in b2% change in demand.
Step 3: Controlling the impact
Now by controlling the impact we must ensure that cumulative impact of all such cross product should be lesser than the impact of self on overall demand. But why to do that? Imagine that the demand going down even if you decrease the price because your cross products overrule the impact on self-demand. In such scenarios, how do you recommend a price change? It’s almost impossible to come up with any solution if we don’t control the impact of cross products. But what does it mean mathematically?

But how do we achieve this during estimation process? We can use a constrained lasso to ensure the above-mentioned condition. Constrained lasso will ensure that coefficients of individual cross product prices would lie within certain limits so that overall impact doesn’t exceed the impact on self. Another way is to redesign the optimisation problem in regularised regression itself. This gives more flexibility to control every aspect on your own.
How to take care of newly introduced products?
In practical demand forecasting problem, we often struggle to design an ecosystem that can forecast sales for newly introduced products. Because of insufficient data points, we often end up forecasting wrong sales/ wide confidence interval. But what if we try to find out an analogous product and use features of those products as proxy. Let’s try to understand the selection of such analogous products.
We will introduce the concept of Dynamic Time Warping (DTW). DTW is popularly used to identify similarity or temporal distance between two time series. An interesting property of DTW is its flexibility to elongate or shrink based on the problem in hand.
Generalised distance between two time series objects X and Y (generated from the same distribution of data) can be written as

This is also known as Minkowski distance. For P=2, d(X,Y) can be considered as Euclidean distance.
Now X and Y can have different length i.e., each of them can have different start and end time stamps but the frequency will be the same. As per Yingmin Li et al, point to point alignment and matching relationship between X and Y can be represented by a time warping path

The series length of X and Y are m and n respectively.
Now If we want to consider the lowest cost path, the corresponding DTW distance is required to meet the following criteria.
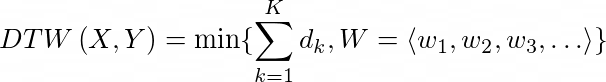
So what does this physically mean? For two different time series we will traverse the temporal path through a sliding way and calculate the distance between them. We will choose the analogous product sequence based on where we get the minimum distance. Now we can have one-to-one matching or one-to-many matching. This means that individual temporal component of the reference series might have either one-to-one match or can have one-to-many match with the analogous sequence. Based on this, construction of the accumulated distance matrix will vary.
Just to summarize the findings here, DTW is a powerful algorithm to identify analogous product of a newly introduced reference product using temporal sequence matching.
Conclusion
In this blog we discussed different challenges of demand forecasting problems and how we can address some of them. Demand forecasting greatly falls under the purview of time series model paradigm and until 2017s, the scope of application of Deep Learning models were restricted only to LSTMs largely. But with the advent of transformer mechanism in NLP, time series researchers tried to bring lot of similar components in structured data space as well. Thus, a new technique called Deep State Space Model (DSSM) was introduced by Rangapuram et al in 2018 which gained lot of popularity in the data science community. One of its popular application found in Kaggle’s M5 forecasting competition hosted by Walmart. It addresses lot of the challenges that we discussed in the blog effortlessly as part of the estimation process itself. Also it’s extremely simple to manage the model complexity since you don’t necessarily have to manage thousands/ millions of forecasting models in the DeepState paradigm. This in turn solves lot of scaling problem that industry is currently struggling with. In our next blog, we will discuss more on the deployment aspect of such demand forecasting models and how we can bring in different architecture to scale up the forecasting engine.
References:
1. https://www.ijcai.org/proceedings/2019/0402.pdf
2. https://www.hindawi.com/journals/mpe/2010/749517/
3. https://stats.idre.ucla.edu/other/mult-pkg/introduction-to-linear-mixed-models/
4. https://mobidev.biz/blog/machine-learning-methods-demand-forecasting-retail

