Generate Sports Rankings with Data Science

In this tutorial, we will go through one very popular algorithm used in generating rankings for sports teams. The method which we will be studying is called Colley Ratings.
Before going into depth, lets first understand why are these ranking systems required. Will a simple win-loss ratio not be enough? To answer this, let’s go through an example. Consider there is a tournament with 4 teams playing in it and following are the results, and final table of the tournament standings so far.

As you can see, Manchester United has won all of their 6 games and sit comfortably on top, Liverpool have lost all their games and lie on bottom of table. Arsenal and Chelsea share the spoil having been defeated by Man Utd in both rounds, defeating Liverpool in both rounds and then splitting the tie between themselves with Arsenal winning in 1st round and Chelsea returning the favour in reverse fixture.
Now imagine we begin 3rd round of fixtures and first couple of game’s results were as below.
Game 1: Arsenal defeat Manchester United
Game 2: Chelsea defeat Liverpool
With that, updated table will look like below.
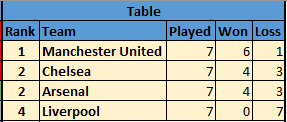
Now wait a minute, does Chelsea and Arsenal really deserve to get same rankings? Isn’t it pretty obvious that Arsenal has defeated Manchester United who were dominant team in the tournament so far, whereas Chelsea defeated Liverpool who had anyways lost all their games. Definitely Arsenal should get more credit and should be ranked higher than Chelsea. But how do we do that? If we are using just a simple win-loss ratio, there is no way to differentiate them. Further on if you are considering goal difference and such, consider that all games have been won by the score line of 2 goals to 1, again we have a deadlock. Then how should we take into account the fact Arsenal defeated a much stronger team than Chelsea did, and hence deserves a higher ranking. This is where ranking systems come into picture. As we will see, Colley rankings are able to understand the event of a strong team being defeated and adjust their rankings accordingly. So without further delay, let’s get started.
Colley Rankings
Mr. Wesley N. Colley suggested that instead of calculating rankings based on win-loss ratio like; ratings = [total wins] / [total games], ratings should be calculated based on following formula
Rating = [1 + total wins] / [2 + total games]. If you look at this formula, before start of any tournament, all teams will begin with a rating of 0.5, as both ‘total wins’ and ‘total games’ will be zero. Keep note of this point (the fact that all teams start with a rating of 0.5), it will come in handy later on. In fact, during all times, the average of all team’s ratings in Colley’s algorithm will always stay at 0.5.
We can write total-wins as shown below.

Looking closely into ½ * [total-games] term for a single team, we can say that ½ * [total-games] = ½ * [1+1+1…1] where ‘1’ stands for a game played against each opponent. This in turn can be written as ½ * [total-games] = [1/2 + ½ + ½+..]. Now if you remember, as said before at the start, rating of all teams would be around 0.5 and hence average rating for all teams combined will also be 0.5. Considering this, we can say that [1/2 + ½ + ½ + ..] ~= [sum of opponent’s ratings]. With this, rewriting equation for total-wins.
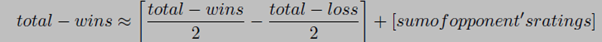
Rewriting formula for ratings,
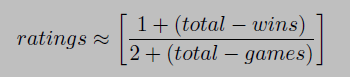
Expanding total-wins and writing down rating for individual team, we can write as.
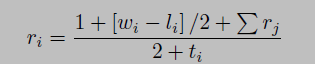
Where rᵢ, wᵢ, lᵢ, and ti represent rating, wins, loss and total game for the team of interest and ∑rj is sum of opponent’s ratings. This can be further rearranged as
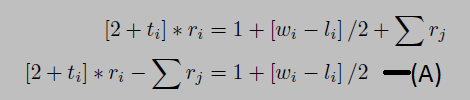
Now, as with most of my other tutorials, let’s use a toy example to understand mathematical equations better. Consider a case of two teams. As stated above, before beginning, they both will have a rating of 0.5 each. Now let’s suppose they played one game against each other. Let rW and rL represent new ratings for winning and loosing team respectively. If you put tᵢ (which will be equal to 1) for both teams, and consider their wᵢ and lᵢ values, we will get following results from equation (A)
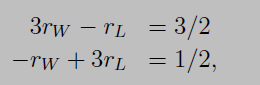
This represents a simple two variable linear system, which when solved gives us our new ratings as rw = 5/8 and rL = 3/8. For 2 teams, equation (A) resulted in two variable linear system, for N teams, it will result in N variable linear system. In programming world, whenever we want to solve N variable linear equations, we always write them in form of a matrix. So rewriting equation (A) in matrix form as
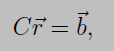
Where vector r represents column-vector of all the ratings rᵢ and vector b is a column-vector of the right-hand-side of equation (A). The matrix C, defined as the Colley Matrix, is just slightly more complicated. Imagine having our four favorite English premier league teams as rows and columns of a 4x4 matrix, as shown in below picture
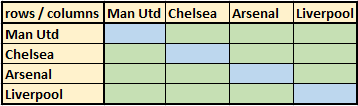
The diagonal elements in Colley matrix should be filled by number = (2 + total-games) for corresponding team. So 1st blue cell should have a value of 2 + number of games played by Manchester United. Similarly rest of cells to be filled for Chelsea, Arsenal and Liverpool games. The off diagonal elements, represented by green cell should have negative value of the number of games played between team represented by row and column for that cell. So for e.g. cell intersecting Man Utd row and Chelsea column should have a number equal to negative value of number of Man Utd vs Chelsea games. And like that we will fill rest of the cells in Colley matrix. Once we solve this N variable linear equation Cr = b, we will get vector value for ‘r’, which represents ratings for each individual team.
With this clear understanding of theoretical background, let’s go ahead and write a Python code to calculate Colley’s rankings for toy example introduced at the beginning of this article. Python code file, along with couple of supporting files can be found at my github repo here.
Before beginning to code, let me explain structure of couple of supporting files, namely ‘scores’ and ‘teams’, both of which are in ‘comma separated value’ format. ‘teams’ file contains list of teams, alongside a ‘number’. This ‘number’ will be used to represent the team in ‘scores’ file. Following screenshot shows contents of ‘teams’ file.

So from now on, whenever we want to represent Manchester United, we will represent them with number 1. Similarly for Chelsea, Arsenal and Liverpool, we will use numbers 2, 3, and 4 respectively while representing them in ‘scores’ file. Now let’s have a look at ‘score’s file with help of following screenshot.
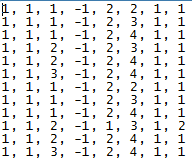
Each row in ‘scores’ file corresponds to a game. I will explain it little later as to why is this file in such a particular order. Columns in ‘scores’ file represent => Column 1 = Number of days since 1/1/0000 when this particular game was played. Column 2 = today’s date. Column 3 = team 1 number. Column 4 = team 1 ‘home’ value (1 = home game, -1 = away game, 0 = neutral). Column 5 = team 1 score. Column 6 = team 2 number. Column 7 = team 2 ‘home’ value (1 = home game, -1 = away game, 0 = neutral). Column 8 = team 2 score.
As we will not be using Column 1, 2, 4 and 7 values in this exercise, I have put dummy numbers for them. Also, just for my convenience I have kept score (Column 5 for team 1 score and Column 8 for team 2 score) as mostly 2 and 1 each, as we will not be looking into scores either in this example. We will just use it to determine winner of each game.
Let’s take example of first row. Column 1 and 2 representing date of the game has dummy values of ‘1’ each. Column 3 has a value of ‘1’. Cross checking this with our ‘teams’ file, we can see that value of ‘1’ is used to represent Manchester United. Column 4 has ‘-1’, signifying that this game was away game for Manchester United. Col 5 has a value of ‘2’ meaning that 2 goals were scored by Manchester United. Col 6 value represent team 2 number, where number 2 means team 2 was Chelsea and this was a Manchester United vs Chelsea game. Col 7 has a value of ‘1’ meaning to say this was a home game for Chelsea and final column has a value of ‘1’ representing number of goals scored by Chelsea.
Finally, let’s start to code this algorithm. Coding Colley algorithm is relatively simple and fairly self explanatory. As with any Python file, we will import required packages, namely numpy and pandas in this case.
# Importing packages
import numpy as np
import pandas as pdThen we go and read ‘teams’ and ‘scores’ files.
# Reading 'teams' and 'scores' data
teams = pd.read_csv('teams.txt', header = None)
num_of_teams = len(teams.index)data = pd.read_csv('scores.txt', header = None)
We initialize Colley matrix and vector b with all 0 in required dimensions.
# Initializing Colley Matrix 'c'and vector 'b'
c = np.zeros([num_of_teams, num_of_teams])
b = np.zeros(num_of_teams)Then, iterating through ‘scores’ file line by line, we populate Colley matrix and vector ‘b’ depending on which teams are playing and winner of each game.
# Iterating through rows and populating Colley matrix values
for index, row in data.iterrows():
t1 = row[2]
t2 = row[5]
c[(t1-1)][(t1-1)] = c[(t1-1)][(t1-1)] + 1 # Updating diagonal element
c[(t2-1)][(t2-1)] = c[(t2-1)][(t2-1)] + 1 # Updating diagonal element
c[(t1-1)][(t2-1)] = c[(t1-1)][(t2-1)] - 1 # Updating off - diagonal element
c[(t2-1)][(t1-1)] = c[(t2-1)][(t1-1)] - 1 # Updating off - diagonal element
# Updating vecotr b based on result of each game
if row[4] > row[7]:
b[(t1-1)] += 1
b[(t2-1)] -= 1
elif row[4] < row[7]:
b[(t1-1)] -= 1
b[(t2-1)] += 1Once that is done, we make the adjustment of adding 2 to diagonal elements of Colley matrix and dividing and adding 1 to each element of vector b, as per equation (A).
# Adding 2 to diagonal elements (total number of games) of Colley matrix
diag = c.diagonal() + 2
np.fill_diagonal(c, diag)# Dividing by 2 and adding one to vector b
for i, value in enumerate(b):
b[i] = b[i] / 2
b[i] += 1
Afterwards we solve this N variable linear equation using numpy’s linalg.solve().
# Solving N variable linear equation
r = np.linalg.solve(c, b)Once we get result in ‘r’, we display top 4 teams by using argsort() method.
# Displaying ranking for top 4 teams
top_teams = r.argsort()[-4:][::-1]
for i in top_teams:
print (str(r[i]) + " " + str(teams.iloc[i][1]))And with that, if you successfully downloaded the repo and ran this code, you should see following output.

Now, to check real strength of this algorithm, we will be adding two more games in our ‘scores’ files by inserting following lines.
Game 1: Arsenal defeat Manchester United => 1, 1, 1, -1, 1, 3, 1, 2
Game 2: Chelsea defeat Liverpool => 1, 1, 2, -1, 2, 4, 1, 1
Running Python file again after making above modifications in ‘scores’, you will get following result.

As you can see, even though Arsenal and Chelsea have played, won and loss equal number of games, Colley algorithm was able to recognize the fact that Arsenal had defeated a stronger team in Manchester United compared to Liverpool who was defeated by Chelsea.
The In-Form Team
Coming back to the format of ‘scores’ files, let’s see how it is useful with one more use case. Consider there are 3 rounds in tournament with results shown in below image.

Manchester United win all their games in round 1, Chelsea win all their games in round 2, and Arsenal in round 3. Although all 3 teams are tied on number of wins, any knowledgeable sports person will tell you that after winning all games in first round, Man Utd have fizzled out. Arsenal on the other hand are on a hot streak winning all their games in latest round of fixtures, and Chelsea lie in between. With this in mind, even though total points for Man Utd, Arsenal and Chelsea are same, a good ranking system should provide a provision to distinguish old performances against recent one.
To take this ‘momentum’ or ‘in-form’ factor into account, a new variable called ‘weight’ is introduced. With the help of a simple ‘if else’ conditional statements, we are giving different weightage to different games.
# Iterating through rows and populating Colley matrix values
for index, row in data.iterrows():
t1 = row[2]
t2 = row[5]
if row[0] <= 6: #For first round matches
weight = 0.9
elif row[0] > 6 and row[0] <=12: #For second round matches
weight = 1.0
else:
weight = 1.1 #For third round matches
c[(t1-1)][(t1-1)] = c[(t1-1)][(t1-1)] + 1 * weight # Updating diagonal element
c[(t2-1)][(t2-1)] = c[(t2-1)][(t2-1)] + 1 * weight # Updating diagonal element
c[(t1-1)][(t2-1)] = c[(t1-1)][(t2-1)] - 1 * weight # Updating off - diagonal element
c[(t2-1)][(t1-1)] = c[(t2-1)][(t1-1)] - 1 * weight # Updating off - diagonal element
# Updating vecotr b based on result of each game
if row[4] > row[7]:
b[(t1-1)] += 1 * weight
b[(t2-1)] -= 1 * weight
elif row[4] < row[7]:
b[(t1-1)] -= 1 * weight
b[(t2-1)] += 1 * weightAs the tournament progress, less weightage is given to old games. Whereas latest round of fixtures are given higher weightage compared to previous two rounds. With above modification, if we again run our Colley algorithm, we will get following results.
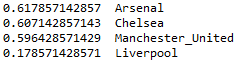
As expected, Arsenal having won all its games in latest fixtures are ranked first, whereas Man Utd are ranked third even though they share same points with Arsenal and Chelsea.
And with that, I will draw curtains on this article. Hope the sports fanatic and Data scientist in you was able to appreciate the beauty and simplicity of Colley’s method.
As usual, if you liked this post, Follow, Like, Retweet it on Twitter or Claps, Likes here on Medium will act as encouragement for writing new posts as I continue my journey into Blogging world.
Till next time….cheers!!