Easy Distribution-Free Conformal Intervals for Time Series
Using Python and your test set to derive distribution-agnostic intervals
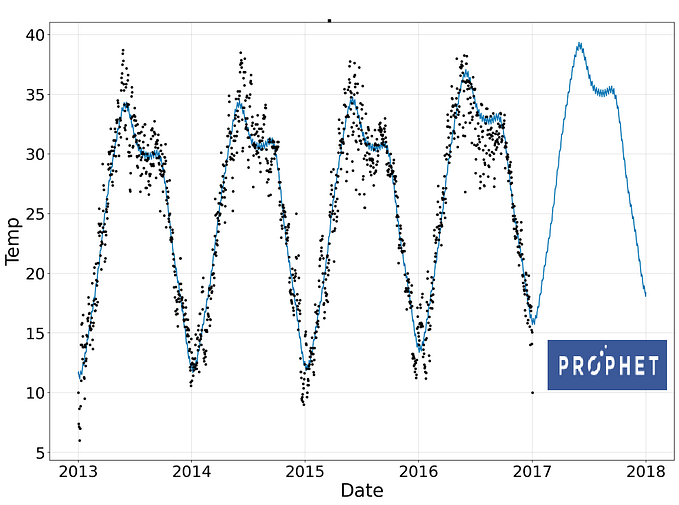
As important as producing a point estimate for forecasting applications is determining how far off the actual value is likely to be from the prediction. Most forecasts are not 100% accurate so having a good sense of the possibilities when dealing with model implementation becomes crucial. For models with underlying functional forms, such as ARIMA, confidence intervals can be determined using the assumed distribution of the residuals and the standard errors of the estimation. These intervals are logical in that they expand the further out from the known last value a forecast goes — as uncertainty accumulates, this becomes represented in a mathematical way that gels with our intuitions. And if the model assumptions hold, a 95% confidence interval is guaranteed to contain 95% of the actual values.
Conformal Prediction
However, when dealing with a machine learning model that has no form that can be represented with a simple equation and assumes no distribution in the underlying data, creating a sound confidence interval becomes more of a challenge. A popular solution to this problem are conformal predictions. The GitHub repository, Awesome Conformal Prediction…