One of the challenges that arise when developing machine learning models for classification is class imbalance. Most of the machine learning algorithms for classification were developed assuming balanced classes however, in real life it is not common to have properly balanced data. Due to this, various alternatives have been proposed to address this problem as well as tools to apply these solutions. Such is the case imbalanced-learn [1], a python library that implements the most relevant algorithms to tackle the problem of class imbalance.
In this blog we are going to see what class imbalance is, the problem of implementing Accuracy as a metric for unbalanced classes, what random under-sampling and random over-sampling is and imbalanced-learn as an alternative tool to address the class imbalance problem in an appropriate way. Then, the blog will be divided as follows:
- What is class imbalance?
- The accuracy paradox
- Under-sampling and Over-sampling
- Imbalanced-learn in practice
What is class imbalance?
The problem of class imbalance arises when the samples for each class are unbalanced, that is, there is no balanced ratio between the distribution of the classes. This imbalance can be slight or strong. Depending on the sample size, ratios from 1:2 to 1:10 can be understood as a slight imbalance and ratios greater than 1:10 can be understood as a strong imbalance. In both cases, the data with the class imbalance problem must be treated with special techniques such as under-sampling, over-sampling, cost-sensitive, among others. Later, we’ll cover under-sampling and over-sampling as well as their implementation with imblearn [1].
The accuracy paradox
One of the underlying things to consider when dealing with unbalanced data in a classification problem is the metric to use. Accuracy is commonly used as the de facto metric, however for the class imbalance problem it would not be a good option since accuracy could be misleading, this problem is better known as the accuracy paradox. Let’s take a look at Figure 2 for a better understanding of the accuracy paradox.

When using accuracy as the metric to evaluate a machine learning model that was trained with a dataset with the class imbalance problem, the results can be misleading. As we can see, the accuracy is 92%, which would make us assume that the model is good enough. However, if we observe in detail we can see that the model learned to classify everything towards class 0, which generates that effect of having a good enough accuracy. In these cases, in addition to applying some method to fix the class imbalance problem, it is suggested to introduce other evaluation Metrics such as precision, recall and F1-Score. Let’s take a look at Figure 3 to better understand how the precision, recall and F1-Score metrics help us to have a better perspective of the results.

Let’s see what just happened. Accuracy is a metric that measures the balance between the true positives and the true negatives, however, when the dataset presents the class imbalance problem, the model will most likely learn to classify everything towards the dominant class, in this case towards class 0. Therefore, even if the model had classified 100% of the data towards class 0, the accuracy would be good enough given that the number of true negatives is dominant. This is why the accuracy metric is often misleading when there is a class imbalance problem (accuracy paradox).
The precision metric measures: "of all the elements that the model classified as positive, how many were actually correct." As we observed, the precision was perfect which would make us think "well, the accuracy and precision are good enough", however it is not entirely correct since of the 10 elements of class 1, only 2 were classified correctly, that is, 8 were classified incorrectly, this can be observed in the recall metric.
The recall metric measures: "the balance between those classified in the positive class by the model with respect to those classified in the negative class but which were actually positive". As we can see, the recall value is very low which gives us a signal that something is not right, that is, several samples that were really positive were classified as negative. In a real context, let’s imagine that the positive class refers to "having cancer" and the negative class refers to "not having cancer", in this context we would be classifying many people who really have cancer as people who do not, which would a catastrophic mistake.
Finally, to generalize the precision and recall metrics, we implement the F1-Score metric, which is understood as "the harmonic mean" between the precision and recall, in other words, it provides a ratio between both metrics. As we can see, the F1-Score value is very low, which is another indicator that something is not right (in our example, the precision is perfect but recall is very poor).
Well, up to this point we have already seen what the class imbalance problem is, some consequences of working with unbalanced classes and some metrics to consider when evaluating models that present the class imbalance problem. Now let’s see some alternatives that can be approached to adjust the class imbalance, specifically let’s see the effect of applying under-sampling and over-sampling based techniques.
Under-sampling and Over-sampling
As we have already seen, the class imbalance problem arises when there is no balance between the class distributions, that is, one or more classes can be dominant with respect to one or more remaining classes. Intuitively this problem can be fixed by adding samples to minority classes, removing samples from majority classes, or a combination of both. So, the process of removing samples from the majority class is known as under-sampling and the process of adding samples to the minority class is called over-sampling.
Random Under-sampling refers to the random sampling of the majority class. This process is carried out until a balance is reached with respect to the minority class. While this technique helps to create a balance between the majority and minority class, it is possible that important information is lost when removing samples from the majority class.
Random Over-sampling refers to the random duplication of samples from the minority class. The addition process is carried out until reaching a balance with respect to the majority class, however, this technique can cause the model to be trained to be overfitted towards the minority class.
Random Under-sampling and Random Over-sampling can be understood as basic techniques to address a class imbalance problem. Today there are more promising techniques that try to improve the disadvantages of random-based approaches, such as synthetic data augmentation (SMOTE [2], ADASYN [3]) or clustering-based under-sampling techniques (ENN [4]).
Well, we already knew what techniques based on under-sampling and over-sampling are, let’s see how to carry them out in practice!
Imbalanced-learn in practice
Imbalanced-learn is an open-source Python library [5] developed by Guillaume Lemaître et.al. [6] which provides a suite of algorithms for treating the class imbalance problem. Such a suite of algorithms is organized into 4 groups: under-sampling, over-sampling, combination of over and under-sampling and ensemble learning methods. For our purposes, on this occasion we will only use the under-sampling and over-sampling extensions.
The example shown below will use an unbalanced dataset. A machine learning model (decision tree) will be trained and the metrics accuracy, precision, recall and f1-score will be evaluated. Subsequently, the under and over-sampling algorithms will be applied and the aforementioned metrics will be evaluated again to make a comparison between the results obtained when training a model without fixing the imbalance problem and those obtained when applying under and over sampling.
So let’s first generate an unbalanced toy dataset:
The unbalanced dataset generated would look like the one shown in Figure 4:
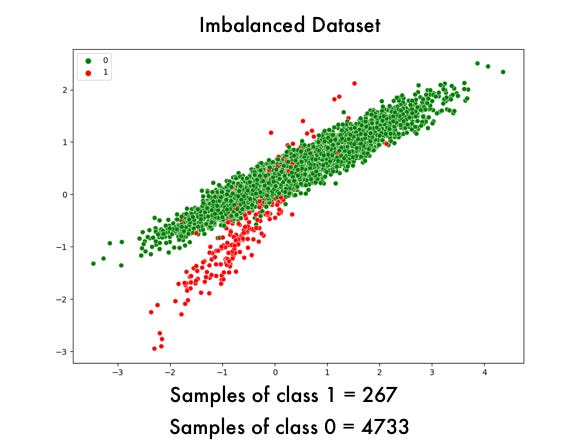
As we can see, the generated dataset presents the problem of class imbalance with a ratio of 1:10. Before applying the under-sampling and over-sampling algorithms, we are going to define a function to be able to train a decision tree with the fixed datasets.
As we have already observed, the function implements the Stratified K-fold cross validation technique in order to maintain the same balance between classes for each fold.
In order to carry out a demonstrative comparison, we are going to define a set of functions which apply each of the sampling algorithms (random over and under sampling), SMOTE as well as a dummy version (which trains the decision tree without considering the class imbalance problem).
The dummy function (line 6), trains a decision tree with the data generated in Code Snippet 1 without considering the class imbalance problem. Random under-sampling is applied on line 10, random over-sampling is applied on line 17 and SMOTE is applied on line 25. In Figure 5 we can see how the class balance was transformed when applying each algorithm.

As we can see, the under-sampling algorithm removed samples from the majority class, aligning it with the minority class. On the other hand, the over-sampling algorithm duplicated elements of the minority class (if you can see, the graph looks similar to the graph in Figure 4). Finally SMOTE (a data augmentation technique), increased the samples of the minority class until it balanced with the majority class. Results are shown in Figure 6.
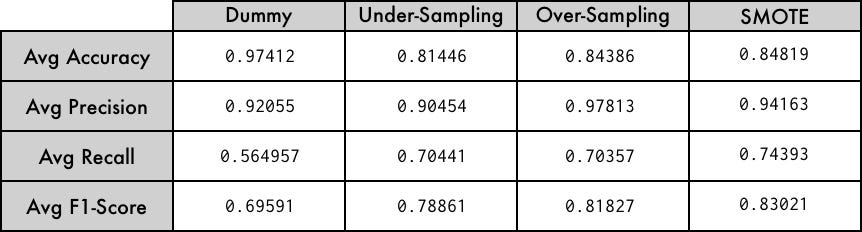
As we can see, the effectiveness of the model improves when applying techniques to correct the class balance problem. For this particular example, the technique based on augmentation of synthetic data (SMOTE) showed better results. At the end of the day, the technique to implement will depend entirely on the data you are working with. It is important to mention that imbalanced-learn provides a wide variety of algorithms to address the problem of unbalanced classes, it is worth taking a look at its documentation [1].
Conclusion
In this blog we saw what the problem of class imbalance is as well as the metrics that must be considered when working with an unbalanced dataset. We also saw an example of how to fix the class imbalance problem using algorithms based on sampling and data augmentation. We also made use of the imbalanced-learn library to extend the algorithms used in the example.
References
[1] https://imbalanced-learn.org/stable/user_guide.html
[2] SMOTE: Synthetic Minority Over-sampling Technique
[3] ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning
[4] Aymptotic Properties of Nearest Neighbor Rules Using Edited Data
[5] https://github.com/scikit-learn-contrib/imbalanced-learn
[6] Imbalanced-learn: A Python Toolbox to Tackle the Curse of Imbalanced Datasets in Machine Learning





