A Gentle Introduction to Maximum Likelihood Estimation and Maximum A Posteriori Estimation
Getting intuition of MLE and MAP with a football example
Maximum Likelihood Estimation (MLE) and Maximum A Posteriori (MAP) estimation are method of estimating parameters of statistical models.
Despite a bit of advanced mathematics behind the methods, the idea of MLE and MAP are quite simple and intuitively understandable. In this article, I’m going to explain what MLE and MAP are, with a focus on the intuition of the methods along with the mathematics behind.
Example: Probability that Liverpool FC wins a match in the next season
In 2018-19 season, Liverpool FC won 30 matches out of 38 matches in Premier league. Having this data, we’d like to make a guess at the probability that Liverpool FC wins a match in the next season.
The simplest guess here would be 30/38 = 79%, which is the best possible guess based on the data. This actually is an estimation with MLE method.
Then, assume we know that Liverpool’s winning percentages for the past few seasons were around 50%. Do you think our best guess is still 79%? I think some value between 50% and 79% would be more realistic, considering the prior knowledge as well as the data from this season. This is an estimation with MAP method.
I believe ideas above are pretty simple. But for more precise understanding, I will elaborate mathematical details of MLE and MAP in the following sections.
The model and the parameter
Before going into each of methods, let me clarify the model and the parameter in this example, as MLE and MAP are method of estimating parameters of statistical models.
In this example, we’re simplifying that Liverpool has a single winning probability (let’s call this as θ) throughout all matches across seasons, regardless of uniqueness of each match and any complex factors of real football matches. On the other words, we’re assuming each of Liverpool’s match as a Bernoulli trial with the winning probability θ.
With this assumption, we can describe probability that Liverpool wins k times out of n matches for any given number k and n (k≤n). More precisely, we assume that the number of wins of Liverpool follows binomial distribution with parameter θ. The formula of the probability that Liverpool wins k times out of n matches, given the winning probability θ, is below.

This simplification (describing the probability using just a single parameter θ regardless of real world complexity) is the statistical modelling of this example, and θ is the parameter to be estimated.
From the next section, let’s estimate this θ with MLE and MAP.
Maximum Likelihood Estimation
In the previous section, we got the formula of probability that Liverpool wins k times out of n matches for given θ.
Since we have the observed data from this season, which is 30 wins out of 38 matches (let’s call this data as D), we can calculate P(D|θ) — the probability that this data D is observed for given θ. Let’s calculate P(D|θ) for θ=0.1 and θ=0.7 as examples.
When Liverpool’s winning probability θ = 0.1, the probability that this data D (30 wins in 38 matches) is observed is following.

P(D|θ) = 0.00000000000000000000211. So, if Liverpool’s winning probability θ is actually 0.1, this data D (30 wins in 38 matches) is extremely unlikely to be observed. Then what if θ = 0.7?

Much higher than previous one. So if Liverpool’s winning probability θ is 0.7, this data D is much more likely to be observed than when θ = 0.1.
Based on this comparison, we would be able to say that θ is more likely to be 0.7 than 0.1 considering the actual observed data D.
Here, we’ve been calculating the probability that D is observed for each θ, but at the same time, we can also say that we’ve been checking likelihood of each value of θ based on the observed data. Because of this, P(D|θ) is also considered as Likelihood of θ. The next question here is, what is the exact value of θ which maximise the likelihood P(D|θ)? Yes, this is the Maximum Likelihood Estimation!
The value of θ maximising the likelihood can be obtained by having derivative of the likelihood function with respect to θ, and setting it to zero.

By solving this, θ = 0,1 or k/n. Since likelihood goes to zero when θ= 0 or 1, the value of θ maximise the likelihood is k/n.

In this example, the estimated value of θ is 30/38 = 78.9% when estimated with MLE.
Maximum A Posteriori Estimation
MLE is powerful when you have enough data. However, it doesn’t work well when observed data size is small. For example, if Liverpool only had 2 matches and they won the 2 matches, then the estimated value of θ by MLE is 2/2 = 1. It means that the estimation says Liverpool wins 100%, which is unrealistic estimation. MAP can help dealing with this issue.
Assume that we have a prior knowledge that Liverpool’s winning percentage for the past few seasons were around 50%.
Then, without the data from this season, we already have somewhat idea of potential value of θ. Based (only) on the prior knowledge, the value of θ is most likely to be 0.5, and less likely to be 0 or 1. On the other words, the probability of θ=0.5 is higher than θ=0 or 1. Calling this as the prior probability P(θ), and if we visualise this, it would be like below.
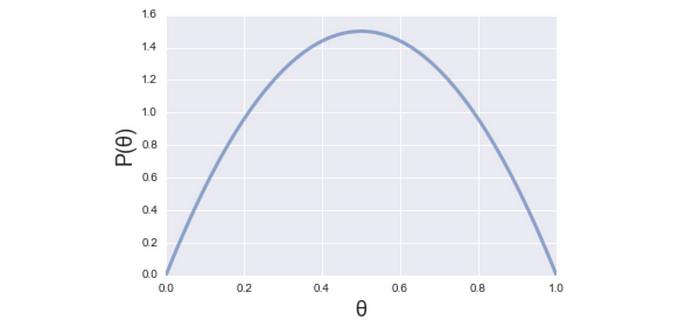
Then, having the observed data D (30 win out of 38 matches) from this season, we can update this P(θ) which is based only on the prior knowledge. The updated probability of θ given D is expressed as P(θ|D) and called the posterior probability.
Now, we want to know the best guess of θ considering both our prior knowledge and the observed data. It means maximising P(θ|D) and it’s the MAP estimation.

The question here is, how to calculate P(θ|D)? So far in this article, we checked the way to calculate P(D|θ) but haven’t seen the way to calculate P(θ|D). To do so, we need to use Bayes’ theorem below.

I don’t go deep into Bayes’ theorem in this article, but with this theorem, we can calculate the posterior probability P(θ|D) using the likelihood P(D|θ) and the prior probability P(θ).
There’s P(D) in the equation, but P(D) is independent to the value of θ. Since we’re only interested in finding θ maximising P(θ|D), we can ignore P(D) in our maximisation.

The equation above means that the maximisation of the posterior probability P(θ|D) with respect to θ is equal to the maximisation of the product of Likelihood P(D|θ) and Prior probability P(θ) with respect to θ.
We discussed what P(θ) means in earlier part of this section, but we haven’t go into the formula yet. Intrinsically, we can use any formulas describing probability distribution as P(θ) to express our prior knowledge well. However, for the computational simplicity, specific probability distributions are used corresponding to the probability distribution of likelihood. It’s called conjugate prior distribution.
In this example, the likelihood P(D|θ) follows binomial distribution. Since the conjugate prior of binomial distribution is Beta distribution, we use Beta distribution to express P(θ) here. Beta distribution is described as below.

Where, α and β are called hyperparameter, which cannot be determined by data. Rather we set them subjectively to express our prior knowledge well. For example, graphs below are some visualisation of Beta distribution with different values of α and β. You can see the top left graph is the one we used in the example above (expressing that θ=0.5 is the most likely value based on the prior knowledge), and the top right graph is also expressing the same prior knowledge but this one is for the believer that past seasons’ results are reflecting Liverpool’s true capability very well.

A note here about the bottom right graph: when α=1 and β=1, it means we don’t have any prior knowledge about θ. In this case the estimation will be completely same as the one by MLE.
So, by now we have all the components to calculate P(D|θ)P(θ) to maximise.

As same as MLE, we can get θ maximising this by having derivative of the this function with respect to θ, and setting it to zero.

By solving this, we obtain following.

In this example, assuming we use α=10 and β=10, then θ=(30+10–1)/(38+10+10–2) = 39/56 = 69.6%
Conclusion
As seen in the example above, the ideas behind the complicated mathematical equations of MLE and MAP are surprisingly simple. I used a binomial distribution as an example in this article, but MLE and MAP are applicable to other statistical models as well. Hope this article helped you to understand MLE and MAP.








